jds17
- 7
- 1
There is a nice problem in Taylor: Classical Mechanics of a puck sliding without friction down a sphere in a uniform gravitational field (problem 4.8).
The question there was at which height the puck takes off from the sphere, which is not hard to solve using conservation of energy.
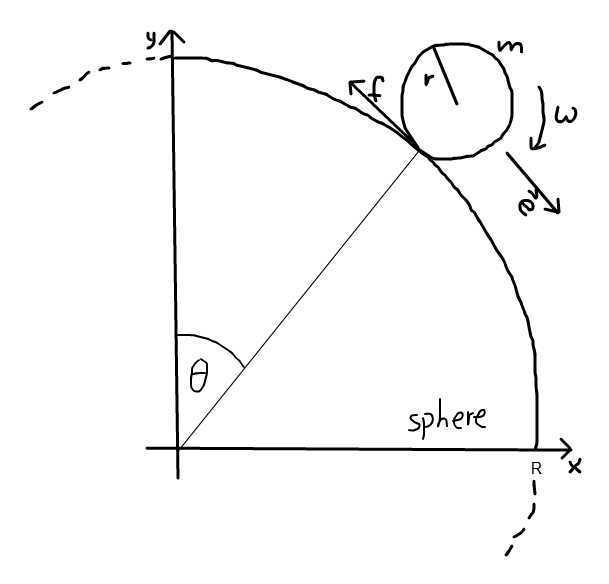
This problem inspired me to try to solve the following problem: Let there be given a fixed sphere of radius ##R##, a gravitational field of strength
##g##, an object of mass ##m##, moment of inertia ##I## and circular cross section of radius ##r## (e.g. a hollow or solid sphere, a cylinder, a disk or
a hoop) which is initially placed on the top of the sphere. We assume static friction between the sphere and the object, the coefficient of static
friction being ##\mu##. We nudge the object a little so that it starts to roll down the sphere.
The question is: Determine what happens first and at which angle:
the object starts to slip on the sphere (and energy starts to dissipate via heat, so there is not much left to say after that moment) or
the object takes off from the sphere
What I could find out so far ist the following:
The angle at which slipping sets in, assuming that the object reaches this angle before detaching from the sphere.
A differential equation the angle ##\theta## measuring the angular displacement from the top (see image) satisfies while the object is rolling.
I would love to get your comments on the correctness of my derivations and be very happy if you could find out more about this problem since obviously
the main question remains unanswered. (Numerical experiments are welcome if they shed a light on the problem, I have not yet tried this.) There exist
similar problems where an object rolls down an incline, but these are much simpler since the angle the surface of the incline makes with the horizon is
the same everywhere, whereas in the case of the sphere it changes from point to point.
So here is my analysis so far:
(A) The angle at which slipping sets in:
Consider a moment in time when the object has rolled around the sphere for a certain angle ##\theta## (see the image). At that time, let ##f## be the
magnitude of the force of static friction, and ##a \vec e## the acceleration of the center of mass of the rolling object, where ##\vec e## is the unit
vector of the momentary direction of motion.
We have ##m a = m g \sin(\theta) - f##. The only torque on the object comes from the static friction, so ##I \dot \omega = r f##. Since the body is
rolling, the distance traveled by a point on its circumference is the same as the displacement of its center, so ##a = r \dot \omega##.
Using these two relations, we get ##m a = m g \sin(\theta) - \frac{I \dot\omega}{r} = m g \sin(\theta) - \frac{I a}{r^2}##, ##(m + \frac{I}{r^2}) a = m
g \sin(\theta)##, ##a = \frac{g \sin(\theta)}{1+\frac{I}{mr^2}}##.
We can now calculate ##f## as follows: ##f = m g \sin(\theta) - m a = m g \sin(\theta) (1-\frac{1}{1+\frac{I}{mr^2}}) = m g \sin(\theta) (1-\frac{mr^2}
{mr^2+I}) = m g \sin(\theta) \frac{I}{mr^2+I}##.
Now, since by definition of ##\mu##, the force of static friction ##f## is constrained as follows: ##f \le \mu m g \cos(\theta)##, we conclude from the
expression we found for ##f## that ##\tan(\theta) \le \mu \frac{mr^2+I}{I}##, i.e. ##\theta \le \arctan(\mu(1+\frac{mr^2}{I})) =: \theta_{max}##.
For example, we get the following values for the angle ##\theta_{max}## at which slipping must set in:
hoop: ##I = m r^2, \theta_{max} = \arctan(2\mu)##
solid ball: ##I = \frac{2}{5} mr^2, \theta_{max} = \arctan(\frac{7}{2}\mu)##
spherical shell: ##I=\frac{2}{3} mr^2, \theta_{max} = \arctan(\frac{5}{2}\mu)##
(B) A differential equation for ##\theta##:
We consider a moment of time at which the object has been rolling on the sphere since the beginning of its motion. Choosing the gravitational potential
energy to be ##0## at ##y = 0##, the initial energy of the system is ##E_i = mgR## and the energy at the time when an angle ##\theta## has been reached
is
##E_{\theta} = \frac{1}{2}m v^2 + \frac{1}{2} I \omega^2 + mgR\cos(\theta) = \frac{1}{2}m v^2 + \frac{1}{2} I \frac{v^2}{r^2} + mgR\cos(\theta)##,
so using conservation of energy we get ##2mgR(1-\cos(\theta)) = (m+\frac{I}{r^2})v^2##.
Since ##v^2 = R^2 \dot\theta^2##, we get ##2mg(1-\cos(\theta)) = (m+\frac{I}{r^2})R\dot\theta^2##, so defining the constant ##c := \sqrt(\frac{2mgr^2}
{R(mr^2+I)})## we arrive at the differential equation
##\dot\theta = -c \sqrt(1-\cos(\theta)), \theta(0) = 0##
which holds until the object starts to slip or until it takes off from the sphere, whichever happens first. Feeding this differential equation to Maxima
yielded a very complicated solution from which I could not read anything off. Maybe you can shed a light on the behavior of the solution to this
nonlinear equation.
The question there was at which height the puck takes off from the sphere, which is not hard to solve using conservation of energy.
This problem inspired me to try to solve the following problem: Let there be given a fixed sphere of radius ##R##, a gravitational field of strength
##g##, an object of mass ##m##, moment of inertia ##I## and circular cross section of radius ##r## (e.g. a hollow or solid sphere, a cylinder, a disk or
a hoop) which is initially placed on the top of the sphere. We assume static friction between the sphere and the object, the coefficient of static
friction being ##\mu##. We nudge the object a little so that it starts to roll down the sphere.
The question is: Determine what happens first and at which angle:
the object starts to slip on the sphere (and energy starts to dissipate via heat, so there is not much left to say after that moment) or
the object takes off from the sphere
What I could find out so far ist the following:
The angle at which slipping sets in, assuming that the object reaches this angle before detaching from the sphere.
A differential equation the angle ##\theta## measuring the angular displacement from the top (see image) satisfies while the object is rolling.
I would love to get your comments on the correctness of my derivations and be very happy if you could find out more about this problem since obviously
the main question remains unanswered. (Numerical experiments are welcome if they shed a light on the problem, I have not yet tried this.) There exist
similar problems where an object rolls down an incline, but these are much simpler since the angle the surface of the incline makes with the horizon is
the same everywhere, whereas in the case of the sphere it changes from point to point.
So here is my analysis so far:
(A) The angle at which slipping sets in:
Consider a moment in time when the object has rolled around the sphere for a certain angle ##\theta## (see the image). At that time, let ##f## be the
magnitude of the force of static friction, and ##a \vec e## the acceleration of the center of mass of the rolling object, where ##\vec e## is the unit
vector of the momentary direction of motion.
We have ##m a = m g \sin(\theta) - f##. The only torque on the object comes from the static friction, so ##I \dot \omega = r f##. Since the body is
rolling, the distance traveled by a point on its circumference is the same as the displacement of its center, so ##a = r \dot \omega##.
Using these two relations, we get ##m a = m g \sin(\theta) - \frac{I \dot\omega}{r} = m g \sin(\theta) - \frac{I a}{r^2}##, ##(m + \frac{I}{r^2}) a = m
g \sin(\theta)##, ##a = \frac{g \sin(\theta)}{1+\frac{I}{mr^2}}##.
We can now calculate ##f## as follows: ##f = m g \sin(\theta) - m a = m g \sin(\theta) (1-\frac{1}{1+\frac{I}{mr^2}}) = m g \sin(\theta) (1-\frac{mr^2}
{mr^2+I}) = m g \sin(\theta) \frac{I}{mr^2+I}##.
Now, since by definition of ##\mu##, the force of static friction ##f## is constrained as follows: ##f \le \mu m g \cos(\theta)##, we conclude from the
expression we found for ##f## that ##\tan(\theta) \le \mu \frac{mr^2+I}{I}##, i.e. ##\theta \le \arctan(\mu(1+\frac{mr^2}{I})) =: \theta_{max}##.
For example, we get the following values for the angle ##\theta_{max}## at which slipping must set in:
hoop: ##I = m r^2, \theta_{max} = \arctan(2\mu)##
solid ball: ##I = \frac{2}{5} mr^2, \theta_{max} = \arctan(\frac{7}{2}\mu)##
spherical shell: ##I=\frac{2}{3} mr^2, \theta_{max} = \arctan(\frac{5}{2}\mu)##
(B) A differential equation for ##\theta##:
We consider a moment of time at which the object has been rolling on the sphere since the beginning of its motion. Choosing the gravitational potential
energy to be ##0## at ##y = 0##, the initial energy of the system is ##E_i = mgR## and the energy at the time when an angle ##\theta## has been reached
is
##E_{\theta} = \frac{1}{2}m v^2 + \frac{1}{2} I \omega^2 + mgR\cos(\theta) = \frac{1}{2}m v^2 + \frac{1}{2} I \frac{v^2}{r^2} + mgR\cos(\theta)##,
so using conservation of energy we get ##2mgR(1-\cos(\theta)) = (m+\frac{I}{r^2})v^2##.
Since ##v^2 = R^2 \dot\theta^2##, we get ##2mg(1-\cos(\theta)) = (m+\frac{I}{r^2})R\dot\theta^2##, so defining the constant ##c := \sqrt(\frac{2mgr^2}
{R(mr^2+I)})## we arrive at the differential equation
##\dot\theta = -c \sqrt(1-\cos(\theta)), \theta(0) = 0##
which holds until the object starts to slip or until it takes off from the sphere, whichever happens first. Feeding this differential equation to Maxima
yielded a very complicated solution from which I could not read anything off. Maybe you can shed a light on the behavior of the solution to this
nonlinear equation.