vvanessa
- 2
- 0
Homework Statement
(General Physics - Algebra based)
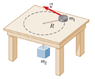
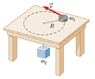
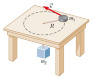
A 0.75 kg puck rotates in a horizontal circular motion on a frictionless table. It is attached to a string that is looped through a hole at the center of table and circular path. Attached to the other end of the string is a 1.5 kg block that is pulled up at a rate of 3 m/s2. What is velocity of the puck?
Knowns
m1 = 0.75 kg
m2 = 1.5 kg
a = 3 m/s2
g = 9.8 m/s2
Unknowns
v (tangential velocity of puck)
Homework Equations
Fw2 = m2g
ac = v2/r
The Attempt at a Solution
∑Fx1 = T = m1ac
⇒ T = m1v2/r
∑Fy2 = T - Fw = m2a
⇒ (m1v2/r) - m2g = m2a
⇒v = √[m2r(a+g)/m1] = √([25.6r m/s2)
How can I find the value of v w/o knowing the radius?
Also, if the block is being pulled up, then doesn't that mean the radius of the circular path where the puck is attached is increasing and, thus, v is increasing over time?