palaphys
- 266
- 17
- Homework Statement
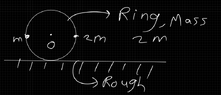
- A ring initially at rest begins to roll (pure rolling) on a rough horizontal floor. It has two masses, m and 2m fixed at diametric points, as shown in the figure. If the mass of the ring is 2m, find the:
1. Angular acceleration of the ring
2. Frictional force acting on the ring
3. Normal reaction on the ring
- Relevant Equations
- Tau= I alpha ,
v= wr
Honestly, I was very confused looking at the problem. With intuition, it is clear that the ring will roll towards the right. But what direction would friction be acting in? That was my first thought.
However I am unable to figure this out, leaving me stuck here.
My only attempt here was to find the com of the ring, which may be useful somehow.
$$\[
\begin{align}
X_{\text{com}} &= \frac{(2m \cdot 0) + (m \cdot (-R)) + (2m \cdot R)}{5m} \\
&= \frac{0 - mR + 2mR}{5m} \\
&= \frac{mR}{5m} \\
&= \frac{R}{5}
\end{align}
$$
I humbly request someone to aid me in this problem and explain the mechanics here, thanks in advance. I'm only used to seeing rings roll where com coincides with geometric center.
However I am unable to figure this out, leaving me stuck here.
My only attempt here was to find the com of the ring, which may be useful somehow.
$$\[
\begin{align}
X_{\text{com}} &= \frac{(2m \cdot 0) + (m \cdot (-R)) + (2m \cdot R)}{5m} \\
&= \frac{0 - mR + 2mR}{5m} \\
&= \frac{mR}{5m} \\
&= \frac{R}{5}
\end{align}
$$
I humbly request someone to aid me in this problem and explain the mechanics here, thanks in advance. I'm only used to seeing rings roll where com coincides with geometric center.