Rotating Wedge & Rise of Mass: Speed Calculation

[hauthuong]

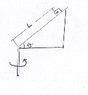
the sloping side is frictionless, it is spun at constant speed by rotating the wedge. show that when a mass rises up the wedge a distance L, the speed of the mass is v=sqr(gLsin0)
I got Fx=m(v^2/r) = mgsin0
v^2=g*sin0*r
can I say r=L ?
I got stuck, could you give me some hints thank you

 

[Pyrrhus]

Hint: Gravity is the centirpetal force because it is pulling the block towards the center.

 

[maverick280857]

What is your specific problem with this? Tried resolving normal reaction in the right direction? Do you know what the radius of the circular path is?

 

[Pyrrhus]

Yes r will be L.

mgsin\theta = m \frac{v^2}{l}

\sqrt{lgsin\theta} = v

 

[hauthuong]

thank you, however, i do not quite understand why r=l. Could you please explain

 

[Himura Kenshin]

Where you get the equation m(v^2/r)=mgsin0. I have search for many reference book but can't find this equation .Can you tell me ?

 

[maverick280857]

Yes r will be L.

mgsin\theta = m \frac{v^2}{l}

\sqrt{lgsin\theta} = v

In my analysis, I resolve the normal reaction in the horizontal and vertical direction. This gives,

N\cos\theta = mg
N\sin\theta = \frac{mv^2}{l\cos\theta}

I divide equation 2 by equation 1 to get

v^2 = gl\sin\theta

Cheers
Vivek

 

[maverick280857]

Where you get the equation m(v^2/r)=mgsin0. I have search for many reference book but can't find this equation .Can you tell me ?

mg sin theta is the component of the weight acting down the incline (resolve mg in two directions one parallel and the other perpendicular to the plane). Drawing a well labeled freebody diagram might help.

 

[Pyrrhus]

Yes Maverick, that's a correct analysys for the way your coordinate system was put, although i prefer your way than mine, because it is using the vertical coordinate system (most used in Circular Motion) rather than the inclined one.