e(ho0n3
- 1,349
- 0
Hallo Alle,
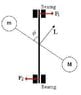
I wish I had a scanner to scan the figure that comes with this problem but anyways...there is a thin massless rigid rod with masses m and M at the ends. This rod is attached to an axle at its center of mass and makes an angle \phi with the axle. The distance of m and M from the point of attachment (call this point the origin O) is r and R respectively. The axle is turning with angular velocity \omega. Oh, and there are bearings at the end of the axle. I hope I've verbalized this properly.
So here is the question: Suppose that M = 0. If the bearings are each a distance d from the point of attachment of the rod and axle, what are the forces at the upper and lower bearings respectively (ignore gravity)?
Now, as I understand it, the angular momentum of this system is always changing direction causing the axle to move around but this movement is 'countered' by the bearings and so I have to calculate the force that will counteract the movement on each bearing.
The angular momentum of the system is
I wish I had a scanner to scan the figure that comes with this problem but anyways...there is a thin massless rigid rod with masses m and M at the ends. This rod is attached to an axle at its center of mass and makes an angle \phi with the axle. The distance of m and M from the point of attachment (call this point the origin O) is r and R respectively. The axle is turning with angular velocity \omega. Oh, and there are bearings at the end of the axle. I hope I've verbalized this properly.
So here is the question: Suppose that M = 0. If the bearings are each a distance d from the point of attachment of the rod and axle, what are the forces at the upper and lower bearings respectively (ignore gravity)?
Now, as I understand it, the angular momentum of this system is always changing direction causing the axle to move around but this movement is 'countered' by the bearings and so I have to calculate the force that will counteract the movement on each bearing.
The angular momentum of the system is
\vec{L} = \vec{r} \times \vec{p}
where\vec{p} = m\vec{v} = m\vec{r} \times \vec{\omega} = mr\omega\sin{\phi}
I can find the torque using \tau = dL/dt and then using \tau = F_{\bot}r to find the forces. My concern is that since the bearings are the same distance d from O, then the forces will have the same magnitude (because of \tau = F_{\bot}r). But I know this can't be since the axle will wobble more on one end that the other if the bearings were not present meaning that one of the bearings much exert more force than other. I just don't get it. Any tips?