- #1
boa_co
- 11
- 0
Hi, all
A plain is flying at a constant velocity v=3 km/s at a constant height above the surface of the Earth, from point A on a Latitude which forms an angle of 20 degrees with the North Pole, to point B which is 5 km north to A.
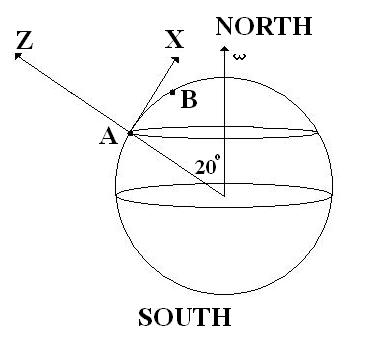
Assuming that B is very close to A so that 20 degrees angle does not change.
At which angle theta does the pilot have to point the airplane relative to the straight line between A and B so that the plaine reaches point B exactly?
(The answer must be in mdeg).
All the forces along the Z -axis are ballanced, the velocity is along the X-axis.
I separated the velocity into two components: North and into the Earth center.
Any diversion in the plain's path is due to Coriolis acceleration so I got something like this:
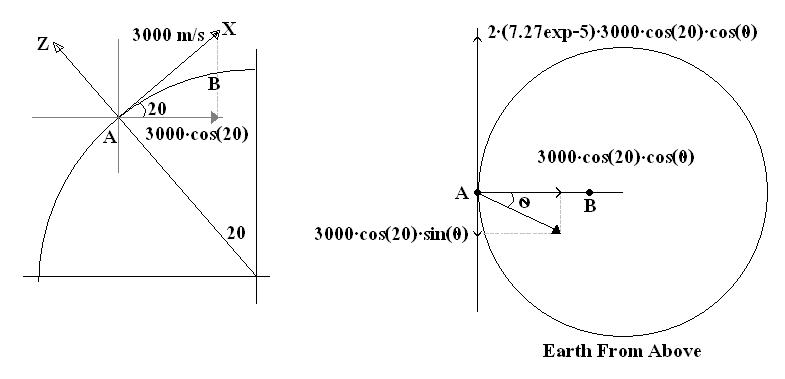
I get the time it takes for the plain to travel from dividing the distance 5 km by the velocity component which results in 5/3*cos(20)*cos(theta). The velocity component we have from the theta angle is opposite to the Coriolis acceleration so that the diversion distance must be 0. Afte plugging the time into the distance equations I get the final result of :
sin(theta)=(7.27exp-5)*(5/3*cos(20))
Unfortunately this is somehow wrong. What am I doing wrong? What am I missing? Why must this be so hard?
Thank you.
Homework Statement
A plain is flying at a constant velocity v=3 km/s at a constant height above the surface of the Earth, from point A on a Latitude which forms an angle of 20 degrees with the North Pole, to point B which is 5 km north to A.
Assuming that B is very close to A so that 20 degrees angle does not change.
At which angle theta does the pilot have to point the airplane relative to the straight line between A and B so that the plaine reaches point B exactly?
(The answer must be in mdeg).
Homework Equations
All the forces along the Z -axis are ballanced, the velocity is along the X-axis.
The Attempt at a Solution
I separated the velocity into two components: North and into the Earth center.
Any diversion in the plain's path is due to Coriolis acceleration so I got something like this:
I get the time it takes for the plain to travel from dividing the distance 5 km by the velocity component which results in 5/3*cos(20)*cos(theta). The velocity component we have from the theta angle is opposite to the Coriolis acceleration so that the diversion distance must be 0. Afte plugging the time into the distance equations I get the final result of :
sin(theta)=(7.27exp-5)*(5/3*cos(20))
Unfortunately this is somehow wrong. What am I doing wrong? What am I missing? Why must this be so hard?
Thank you.