mickonk
- 7
- 0
This my homework:
Input signal to system is:
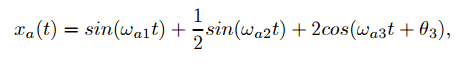
where
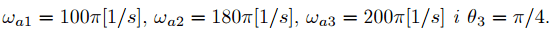

H(exp(jw)) is transfer function of ideal low pass filter with cutoff frequency wg=3*pi/4 and zero phase characteristic. Sampling in A/D converter is done with period T=(1/125) seconds.
a) Calculate output signal ya(t)
b) Calculate sampling period T for ya(t)=xa(t)First thing: they said that wa1, wa2 and wa3 have dimension 1/s. Is that mistake? I think that it should be rad/sec.
I recently started studying digital signal processing and I'm not so good yet but here are my thoughts. I know that A/D sampling period tells us that every T seconds A/D converter will take value from input time signal.
Frequency of sampling would be (1/T) [Hz] and it must be at least two times bigger than biggest frequency in input signal. Ideal low pass filter will pass only signals with frequencies lower than cutoff frequency
I know that I should first find amplitude spectrum of input signal using Fourier transform but I don't know how to find x(n). Here is how I would find FT of input signal. We can write last term of xa(t) as $$\sin (wa3t+(\frac{\pi}{2}+\theta))$$ Fourier transform of sine wave $$A\sin (w_0t)$$ is $$Aj\pi[\delta(w+w_0)-\delta(w-w_0)]$$, So FT of first term of $$x_a(t)$$ will be $$1j\pi[\delta(w+w_{a1})-\delta(w-w_{a1})]$$, FT of second term $$(1/2)j\pi[\delta(w+w_{a2})-\delta(w-w_{a2})]$$. What would be FT for third term, since it is time shifted?
Input signal to system is:
where
H(exp(jw)) is transfer function of ideal low pass filter with cutoff frequency wg=3*pi/4 and zero phase characteristic. Sampling in A/D converter is done with period T=(1/125) seconds.
a) Calculate output signal ya(t)
b) Calculate sampling period T for ya(t)=xa(t)First thing: they said that wa1, wa2 and wa3 have dimension 1/s. Is that mistake? I think that it should be rad/sec.
I recently started studying digital signal processing and I'm not so good yet but here are my thoughts. I know that A/D sampling period tells us that every T seconds A/D converter will take value from input time signal.
Frequency of sampling would be (1/T) [Hz] and it must be at least two times bigger than biggest frequency in input signal. Ideal low pass filter will pass only signals with frequencies lower than cutoff frequency
I know that I should first find amplitude spectrum of input signal using Fourier transform but I don't know how to find x(n). Here is how I would find FT of input signal. We can write last term of xa(t) as $$\sin (wa3t+(\frac{\pi}{2}+\theta))$$ Fourier transform of sine wave $$A\sin (w_0t)$$ is $$Aj\pi[\delta(w+w_0)-\delta(w-w_0)]$$, So FT of first term of $$x_a(t)$$ will be $$1j\pi[\delta(w+w_{a1})-\delta(w-w_{a1})]$$, FT of second term $$(1/2)j\pi[\delta(w+w_{a2})-\delta(w-w_{a2})]$$. What would be FT for third term, since it is time shifted?
Last edited: