nonequilibrium
- 1,412
- 2
Hello,
In "An Introduction to Thermal Physics" Schroeder goes to deduce that for any quasi-static process: W = -PdV (p.21), and then on page 112, with the help of dE = Q + W (= first law of Td.) and dE = TdS - PdV (= the Td. identity), he deduces that Q = TdS for ALL quasi-static processes (reversibility is not a prerequisite).
In class we saw that Q = TdS implies reversibility, but I assume this is wrong, then, because Q = TdS already follows out of "regular" happening quasi-statically and on p.82 Schroeder notes: "A quasistatic process can still be irreversible, however, if there is also heat flowing in or out or if entropy is being created in some other way."
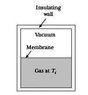
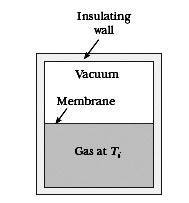
What is an example, then, of a quasistatic, irreversible process? My professor argumented you could let the free (adiabatic) expansion of a gas (i.e. letting a gas freely expand into vacuum in an isolated container (from e.g. half the container volume), so Q = 0 and dE = 0 and W = 0 [see incl. picture for clarity]) happen quasistatically by building brick wall after brick wall (seperating the gas from the vacuum), pulling away each wall after another, letting the gas expand infinitesimally further each go. According to Schroeder, however, this is clearly not quasistatic since W (= 0) does not equal PdV (clearly not zero). Furthermore, if it were quasistatic, then Q = TdS and since Q = 0, the adiabatic expansion would be reversible.
On wikipedia it gave the following example of an irreversible, quasistatic process:
But I must say I don't quite get it, because earlier on the page it defines quasistatic as "the system will go through a sequence of states that are infinitesimally close to equilibrium (so the system remains in quasistatic equilibrium)", while in the example it argues that it cannot be infinitesimally close to equilibrium... If indeed the example itself is a good one, then what is a better definition of quasistatic? (so you don't get a contradiction...)
So what is the deal? AKA what is an irreversible, quasistatic process (so where Q = TdSsystem yet dSuniverse > 0)
Thank you,
mr. vodka
In "An Introduction to Thermal Physics" Schroeder goes to deduce that for any quasi-static process: W = -PdV (p.21), and then on page 112, with the help of dE = Q + W (= first law of Td.) and dE = TdS - PdV (= the Td. identity), he deduces that Q = TdS for ALL quasi-static processes (reversibility is not a prerequisite).
In class we saw that Q = TdS implies reversibility, but I assume this is wrong, then, because Q = TdS already follows out of "regular" happening quasi-statically and on p.82 Schroeder notes: "A quasistatic process can still be irreversible, however, if there is also heat flowing in or out or if entropy is being created in some other way."
What is an example, then, of a quasistatic, irreversible process? My professor argumented you could let the free (adiabatic) expansion of a gas (i.e. letting a gas freely expand into vacuum in an isolated container (from e.g. half the container volume), so Q = 0 and dE = 0 and W = 0 [see incl. picture for clarity]) happen quasistatically by building brick wall after brick wall (seperating the gas from the vacuum), pulling away each wall after another, letting the gas expand infinitesimally further each go. According to Schroeder, however, this is clearly not quasistatic since W (= 0) does not equal PdV (clearly not zero). Furthermore, if it were quasistatic, then Q = TdS and since Q = 0, the adiabatic expansion would be reversible.
On wikipedia it gave the following example of an irreversible, quasistatic process:
An example of a quasistatic process that is not reversible is the slow heat exchange between two bodies at two finitely different temperatures, where the heat exchange rate is controlled by an approximately adiabatic partition between the two bodies (Sears and Salinger, 1986) — in this case, no matter how slowly the process takes place, the states of the two bodies are never infinitesimally close to equilibrium, since thermal equilibrium requires that the two bodies be at precisely the same temperature
But I must say I don't quite get it, because earlier on the page it defines quasistatic as "the system will go through a sequence of states that are infinitesimally close to equilibrium (so the system remains in quasistatic equilibrium)", while in the example it argues that it cannot be infinitesimally close to equilibrium... If indeed the example itself is a good one, then what is a better definition of quasistatic? (so you don't get a contradiction...)
So what is the deal? AKA what is an irreversible, quasistatic process (so where Q = TdSsystem yet dSuniverse > 0)
Thank you,
mr. vodka