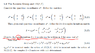helpcometk
- 71
- 0
Homework Statement
I have read the following text in a textbook(look the attaxhement) ,and i have a
simple question .WHY every 2x2 hermitian matrix would have to satisfy this Equation.It is not obvious to me why.Does anyone know the answer?
The textbook stops there without giving any answer.Is it something obvious?
Is there any lengthy calculation to show this?