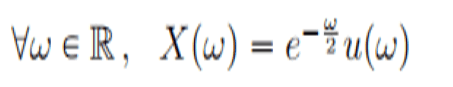Signal & System CTFT: Find x(t) from X(ω)
Click For Summary
Discussion Overview
The discussion revolves around finding the continuous-time signal x(t) from its continuous-time Fourier transform (CTFT) X(ω). Participants are exploring methods and hints to solve this problem, particularly focusing on limits and Fourier transform tables.
Discussion Character
- Exploratory, Technical explanation, Homework-related
Main Points Raised
- One participant presents their approach to finding x(t) but indicates they are stuck at the limit part.
- Another participant suggests looking for hints in a table of Fourier transforms, although they express uncertainty about their professor's coverage of this topic.
- A participant discusses the limit behavior of an exponential expression, stating that as n approaches infinity, the expression converges to -1, while also referencing the behavior of the exponential function in terms of sine and cosine components.
- A later reply reiterates the limit behavior discussed previously but notes that their results do not match the solution provided by their professor, prompting them to seek further verification.
Areas of Agreement / Disagreement
Participants do not appear to reach a consensus, as there are differing approaches and unresolved issues regarding the limits and the correctness of the solutions presented.
Contextual Notes
Participants express uncertainty about the completeness of their methods and the applicability of the Fourier transform tables. There are also indications of missing assumptions or steps in the mathematical reasoning.
Similar threads
- · Replies 2 ·
- · Replies 4 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 6 ·
- · Replies 7 ·
- · Replies 7 ·
- · Replies 2 ·
- · Replies 3 ·