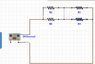
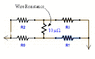Keep in mind that circuit diagrams are not scale models of a physical circuit, they are "schematic" diagrams indicating the topology (in the geometric sense) of the circuit component interconnections. On such a diagram the wires are considered to be perfect conductors, and everywhere reachable by an unbroken path of such wiring is thus at the same potential, so a given contiguous network of such wiring makes a single node.
Unless otherwise specified, a node is treated as a single dimensionless point where all the components connected to that wire join. That means you're free to redraw circuit diagrams, moving the components and wire locations, change wire lengths, straighten bends, add bends, alter their paths, etc,. so long as the topology remains the same. Any component that connects to a given contiguous path can have its connection relocated to any point on the same path without changing the circuit topology.
So for the circuit we're looking at here, the "I" shape wiring joining all the resistors is taken to be a single node at the same potential everywhere. You can treat it as though the wires from all the resistors met at a single point. So yes, we consider that all the currents "mix" and are indistinguishable at the node. UNLESS OTHERWISE INSTRUCTED!
If we were given instructions that the central vertical wire was to be taken as a separately identifiable physical path in the "real world" implementation of the circuit, and that we were required to find the current flowing through that path, then we could apply KCL at the intersections to find the individual currents.
Note well that having the separate path in the physical implementation would not change the overall node potential or the individual resistor currents in any way. So it's generally not worth worrying about how a given conducting path is drawn on paper, or how currents "mix" at a node. As far as we're concerned, all of a given node is at one potential and the sum of the currents entering the node is equal to the sum of the currents leaving it, and that's all the information required to analyze most any circuit.