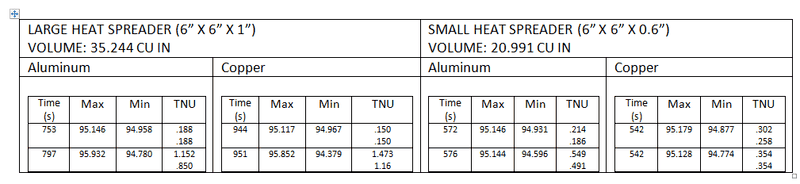
- #1
_Bd_
- 109
- 0
I just ran 2 simulations on Solidworks, same assembly, same initial conditions on all pieces, pretty much I "Cloned" the thermal study and just changed one piece
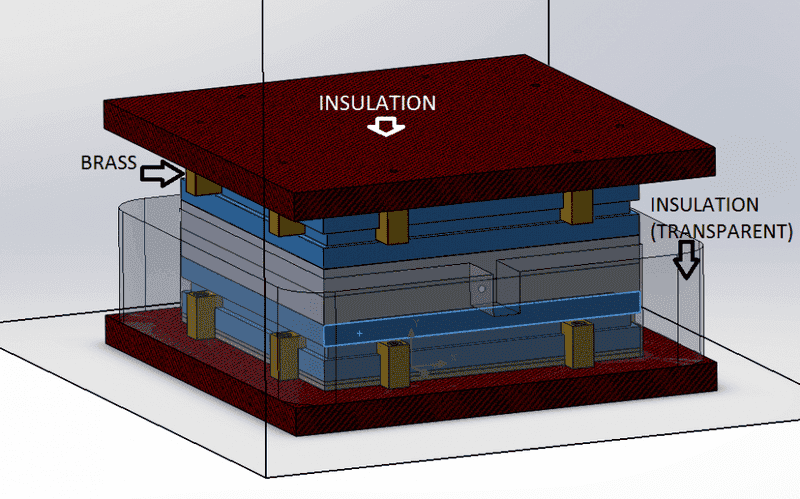
So,
from the assembly above you can see the materials for most pieces, the 2 grey pieces in the center are 2 aluminum plates with a hole in the center and a "probe" at the middle of that hole (this is a temperature-reference point).
For additional clarification, see the cross-section below
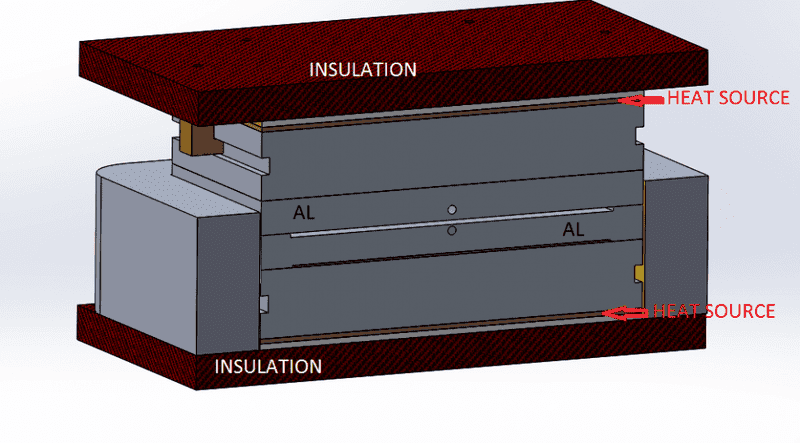
Now, the heat sources are 325 Watts of power each, and the pieces in question (highlighted above) are the only "variant" in both studies, as you can see heat transfers from the heat source to this big block then it transfer to the aluminum pieces.
The purpose of my simulation was to find out what material is better for this big block, Copper or Aluminum?
The obvious answer should be copper, it has less heat capacity (less energy to heat up) and more conductivity (faster response time). *Please feel free to correct me if I'm wrong*
Now, based on those facts about Al vs Cu, it should be obvious that with all other variables the same, the copper should heat up much faster than the Aluminum right?
Well, the Solidworks simulation shows the following results:
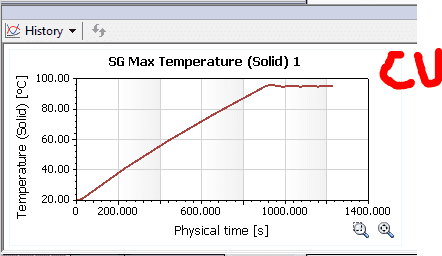
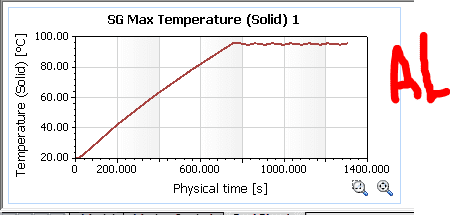
As you can see from the results, the copper seems to be a little more steady (the heat source shuts down after a point reaches 95°C)
However, what really puzzles me is the fact that copper takes roughly 150 extra seconds to heat up to 95, which shouldn't be the case right?
Can someone please help me make sense of this? should I dump solidworks simulation ?
So,
from the assembly above you can see the materials for most pieces, the 2 grey pieces in the center are 2 aluminum plates with a hole in the center and a "probe" at the middle of that hole (this is a temperature-reference point).
For additional clarification, see the cross-section below
Now, the heat sources are 325 Watts of power each, and the pieces in question (highlighted above) are the only "variant" in both studies, as you can see heat transfers from the heat source to this big block then it transfer to the aluminum pieces.
The purpose of my simulation was to find out what material is better for this big block, Copper or Aluminum?
The obvious answer should be copper, it has less heat capacity (less energy to heat up) and more conductivity (faster response time). *Please feel free to correct me if I'm wrong*
Now, based on those facts about Al vs Cu, it should be obvious that with all other variables the same, the copper should heat up much faster than the Aluminum right?
Well, the Solidworks simulation shows the following results:
As you can see from the results, the copper seems to be a little more steady (the heat source shuts down after a point reaches 95°C)
However, what really puzzles me is the fact that copper takes roughly 150 extra seconds to heat up to 95, which shouldn't be the case right?
Can someone please help me make sense of this? should I dump solidworks simulation ?