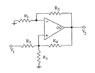
unplebeian said:
If all resistors are = R, then we get a gain of 2
All resistors are not R. R4 is left as a free parameter, and part (a) asks you to sketch the gain as a function of it.
unplebeian said:
Hey farahtc,
I am quite sure of my answer as I even simulated it. I get a gain of 2 and infinity for your questions a and b respectively.
Once again, part a does not ask what the gain is when R4 = R, so I'm not sure why you're plugging that in. I'm also not sure whether you're agreeing or disagreeing with my derivation, but mine is all laid out there, and I'm quite sure it's correct. Not only that but:
1. It is in a simpler form that makes the circuit behaviour at R4 = R/2 much more transparent.
2. It was derived more easily.
3. It is equivalent to what the OP had in the first place, confirming his or her result.
4. It is probably also equivalent to your answer, since it yields the same values for R4 = R/2 and R4 = R.
What I'm trying to say is that I think that this question has been solved, and OP had it right in the first place, and simulation to confirm your result may not have been necessary.
EDIT: Although I can certainly understand your wanting to check your work and see if we were, in fact, all arriving at the same fundamental result. I have no idea how you got your answer: we must have used totally different methods. But you had it correct in the end, after all the algebra!
EDIT 2: Yeah, our answers are the same. All you have to do is plug in R1 = R2 = R3 = R5 = R into your result to end up with my result.