sarah895
- 3
- 0
Homework Statement
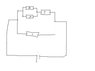
This is the diagram:
https://wug-s.physics.uiuc.edu/cgi/courses/shell/common/showme.pl?cc/DuPage/Phys1202/summer/homework/Ch-21-DC-Circuits/resistor_network/ex1s95p3.gif
R1 = 3W, R2 = 6W, R3 = 11W, R4 =8W, V=6V
A) What is the current through the resistor, R1 in the above circuit? -2A
B) What single, equivalent resistor could replace all of the resistors in this circuit?
C) What is the current supplied by the battery?
D) What is the current through the resistor, R2 ?
Homework Equations
1/R (parallel) = 1/R1 + 1/R2 + 1/R3 + 1/R4
R (series) = R1 + R2 + R3 + R4
E = IR
The Attempt at a Solution
I solved part a. For part be, it seemed to me that R1 and R4 were connected in series, so I combined those two resistors by adding the resistances. Then I added that resistance to R2 and R3 using the equation for parallel resistors.
So, I had: 1/R = (1/11W) + (1/6W) + (1/11W) = 2.87W. This answer is wrong, and I am not sure what to do. Any help would be greatly appreciated :)
Last edited by a moderator: