Solve Pendulum Swing Angle Problem - Physics Adorers

In summary, a pendulum with a length of 2m and a velocity of 3 m/s at its lowest point creates an angle of approximately 39.60 degrees relative to the horizontal. The calculation was based on energy conservation and using the formula mgh=mv^2/2.
  • #1
phunphysics2
29
0
Greetings Physics adorers!

I was wondering if somebody could please check my work for the problem below.

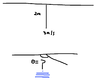
A pendulum with a length 2m has a velocity of 3 m/s at its lowest point. What is the largest angle it creates relative to the horizontal as it swings. Hint: use energy conservation.


Here is my work
mgh=mv^2/2,,,,,,,,,,h=0.459 m,,,,,,,,,cos(angle) = h/r=0.459/2,,,,,,,,,,,angle=76.7 degree


Please let me know if it is correct. If it is wrong, please give suggestions on how I should correct.

Thanks!
 

Attachments

  • pendulum.png
    pendulum.png
    4.3 KB · Views: 632
Physics news on Phys.org
  • #2
The value of h is ok.

But note that cos(angle) = (r - h)/r
 
  • #3
Thank you for your response!

But I am not sure that I understand what you mean
 
  • #4
Refer to the diagram attached.
 

Attachments

  • image.pdf
    10.9 KB · Views: 352
  • #5
Thank you for the diagram! so cos (angle)= (2-.459)/(2)

= about 39.60 degrees?
 

FAQ: Solve Pendulum Swing Angle Problem - Physics Adorers

How do you calculate the period of a pendulum swing?

The period of a pendulum swing is calculated using the equation T=2π√(l/g), where T is the period, l is the length of the pendulum, and g is the acceleration due to gravity.

How does the length of the pendulum affect its swing angle?

The length of a pendulum affects its swing angle by changing the period of the swing. A longer pendulum will have a longer period and therefore a smaller swing angle, while a shorter pendulum will have a shorter period and a larger swing angle.

What is the difference between a simple pendulum and a compound pendulum?

A simple pendulum consists of a single point of mass suspended from a fixed point, while a compound pendulum has a distributed mass and a swinging arm. The equations for calculating the period of a simple pendulum can be used for small swings of a compound pendulum, but for larger swings, a more complex equation must be used.

How does the mass of the pendulum affect its swing angle?

The mass of a pendulum does not affect its swing angle, only its period. According to the equation T=2π√(l/g), the mass does not play a role in the calculation of the period. However, a heavier pendulum will require more force to move, so it may have a slightly smaller swing angle due to air resistance.

What factors can affect the accuracy of the calculated swing angle of a pendulum?

The accuracy of the calculated swing angle of a pendulum can be affected by factors such as air resistance, friction in the pivot point, and the precision of the measurement of the pendulum's length. Additionally, the small angle approximation used in the equation T=2π√(l/g) may not hold true for larger swing angles, leading to a less accurate calculation.

Similar threads

Foucault Pendulum at the North Pole
Replies
9
Views
1K
Swinging Tarzan: Solving for Maximum Height & Angle
Replies
3
Views
2K
For a Pendulum: Knowing Acceleration Find Maximum Angle
Replies
26
Views
2K
How to find the maximum angle of a pendulum after a mass collides with it
Replies
4
Views
3K
Pendulum - Maximum Angle in 2nd half of swing
Replies
3
Views
5K
Tarzan swinging on a vine -- At what angle does the vine break?
Replies
8
Views
3K
Pendulum Swinging Speeds: Solving for Initial Velocity and Angle
Replies
23
Views
2K
Work done on a conical pendulum
Replies
3
Views
2K
Pendulum swinging and hitting a peg
Replies
1
Views
2K
What a I doing wrong? Swing/pendulum Questioj
Replies
8
Views
1K

Hot Threads

Recent Insights

Back
Top