NotaPhysicsMan
- 146
- 0
Alright, here's my Q and A. Please verify 
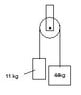
By means of a rope whoe mass is negligible, two blocks are suspended over a pulley, as the drawing shows (attachment). The pulley can be treated as a uniform solid cylindrical disk (I=1/2MR^2) The downard acceleration of the 44.0 kg block is observed to be exactly one-half the acceleration due to gravity. Noting that the tension in the rope is not the same on each side of the pulley, find the mass of the the PULLEY.
Alright, here was my strategy.
Summ of the Torque= (Tension x lever arm )block 1 - (tension x lever arm) block 2)
Sum of torque = moment of inertia x angular acceleration. I=1/2MR^2
Combine two. Tl(block1)- Tl (block 2)= 1/2MR^2 x a
Ok so I don't have Tension 1 or Tension 2. I know the lever arms are basically the radius for each block. I found tension by isolating two situations for the blocks. So for example, block 1:
I know that acceleration (9.81/2) and is positive for B1 and negative for B2.
F=ma or T-W= ma
T=W+ma. I used this to find tension, this tension is equal to the tension on the pulley. so T1 = 162 N, T2=216N.
I have the two T forces.
ok, so plug into equation.
I know that the Radius = lever arm. Also angular acceleration = a/R (sub in.)
TR(block1)- TR (block 2)= 1/2MR^2 x a/R
Ok, I try cancelling the R's.
I get R(T1-T2) = 1/2 MR x a, again the R's cancel.
so 162-216 N =1/2 M x 9.81/2
M= 22kg?
ok, Hopefully I did this right.
By means of a rope whoe mass is negligible, two blocks are suspended over a pulley, as the drawing shows (attachment). The pulley can be treated as a uniform solid cylindrical disk (I=1/2MR^2) The downard acceleration of the 44.0 kg block is observed to be exactly one-half the acceleration due to gravity. Noting that the tension in the rope is not the same on each side of the pulley, find the mass of the the PULLEY.
Alright, here was my strategy.
Summ of the Torque= (Tension x lever arm )block 1 - (tension x lever arm) block 2)
Sum of torque = moment of inertia x angular acceleration. I=1/2MR^2
Combine two. Tl(block1)- Tl (block 2)= 1/2MR^2 x a
Ok so I don't have Tension 1 or Tension 2. I know the lever arms are basically the radius for each block. I found tension by isolating two situations for the blocks. So for example, block 1:
I know that acceleration (9.81/2) and is positive for B1 and negative for B2.
F=ma or T-W= ma
T=W+ma. I used this to find tension, this tension is equal to the tension on the pulley. so T1 = 162 N, T2=216N.
I have the two T forces.
ok, so plug into equation.
I know that the Radius = lever arm. Also angular acceleration = a/R (sub in.)
TR(block1)- TR (block 2)= 1/2MR^2 x a/R
Ok, I try cancelling the R's.
I get R(T1-T2) = 1/2 MR x a, again the R's cancel.
so 162-216 N =1/2 M x 9.81/2
M= 22kg?
ok, Hopefully I did this right.