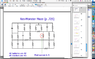
Solve the Res-monster Maze in Minutes!

[sai2020]

Homework Statement

See image. According to Halliday, Resnick and Walker this question takes only a couple of minutes of mental calculation.

Homework Equations

V=IR i guess

The Attempt at a Solution

I tries for hours but no loop..

 

[alphysicist]

Hi sai2020,

When you write out Kirchoff's loop equation for a circuit with only resistors and (ideal) batteries, if you know the values of the battery voltages and the resistors, the only unknowns in your equations are the currents. And the currents in the loop equations only show up when your loop passes through a resistor.

So, looking at your picture, can you start at the resistor, and find some path, following wires through the circuit, that only passes through batteries and ends up back at the resistor? If you can, then writing the loop equation for that path would only have one unknown--the current in the resistor that you are looking for. So what do you get?

 

[shengzhoumi]

This is what you do:

This current will always pick the easiest way to flow, so you know that the loop will have no resistors. If you look at the diagram, there is only one path with no resistors except for resistor R.

When you finish drawing the loop, the loop should look like a screwed up j. It should have 4 batteries too.

After that, just use V=iR to calculate the current.

Happy Solving. :)

 

[sushrutphy]

Hi...sushrut here...
Is the answer coming out to be 2 coulombs?

 

[shengzhoumi]

ya, ur right...good job

 

[sharkasm]

NO! sorry for the screaming, but current is measured in amperes, not coulombs. it does make a difference.(2 is correct though). and Shengzhoumi, current will not always pick the easiest path to flow, it will split up depending on the individual resistances, in fact the solution requires you to go over a resistor, namely R, so your argument that it will have no resistor's is very flawed. what you described was a short circuit. the reason that is the path to follow is that according to kirchhoff the sum of the voltage drops will add to zero in that loop.

 

[supratim1]

look properly, there is a loop with only that resistor and batteries.

 

[Mandeep Deka]

Look at the loop highlighted, it has only the resistor across which current is to be measured, and the cells!
There's a very similar cap-monster maze as well.. always try to find such loops in circuits of this sort!

 

[mkrishnan]

but won't the presence of other batteries and resistors affect the current flow in the resistance 'R'? for example when we use Maxwell's loop current rule; if current through one loop is i1,and in another loop be i2,then current through a common resistor between the loops is given by (i1-i2)!

wont stuff like this happen in this circuit? if not why?!

 

[Whakataku]

To those of you who don't see from the implication, I shall expand.

Look carefully at the circuit, the three emf on the left of the circuit are moving the charge in the clockwise direction, and the one emf on the right is the opposite direction.

So for the sum of emf, don't forget to make the opposing emf have the opposite sign.

Then i = (ε net)/R is self-explanatory.


The devil is in the details :)

 

[agnivesh]

but how is it that when 4 batteries of 4 v each r connected...u get the net emf to be 8 v

 

[agnivesh]

ooops sorry...now i understood...that battery connected in opposite order will hav opposite sign

 

[mdm1984]

Disagree. At the end of the path described, resistor ‘R’ isn’t alone. There are two other resistors next to it (in parallel) right-and-center--AND one of them has an emf. If there was a short circuit, then maybe the three emfs may be ignored. But it's not even a short circuit. So why aren’t the currents through all emfs relevant? I think this problem is tougher than advertised. Someone please do the 18-by-18 matrix. Not it.

 

[gneill]

Disagree. At the end of the path described, resistor ‘R’ isn’t alone. There are two other resistors next to it (in parallel) right-and-center--AND one of them has an emf. If there was a short circuit, then maybe the three emfs may be ignored. But it's not even a short circuit. So why aren’t the currents through all emfs relevant? I think this problem is tougher than advertised. Someone please do the 18-by-18 matrix. Not it.

It doesn't matter what's in parallel with an ideal source (unless it's another ideal source with a different potential, and then FZZZSST! BANG!). Nothing in parallel with that resistor will change the potential across it that's set by the indicated ladder of ideal voltage sources.