Solve Torque & Magnetism: Find Magnetic Field Strength

  • Thread starter Thread starter hover
  • Start date Start date
  • Tags Tags
    Magnetism Torque
AI Thread Summary
The discussion revolves around calculating the magnetic field strength required to prevent a 10-turn wire loop from rotating in a uniform magnetic field while carrying a 2.0 A current. The participant initially attempted to balance the torques acting on the loop, noting that the magnetic field exerts force only on the segments of the wire that are perpendicular to it. After some calculations, they derived the equation B = (mg)/(20IL) and computed a magnetic field strength of 0.1225 Tesla. Ultimately, the participant realized their initial calculation was correct after a brief moment of confusion. The thread highlights the importance of careful calculation in physics problems involving torque and magnetic fields.
hover
Messages
342
Reaction score
0

Homework Statement


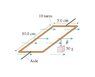
The 10-turn loop of wire shown in the figure lies in a horizontal plane, parallel to a uniform horizontal magnetic field, and carries a 2.0 current. The loop is free to rotate about a nonmagnetic axle through the center. A 50 mass hangs from one edge of the loop.

What magnetic field strength will prevent the loop from rotating about the axle?

Homework Equations


F = ILxB
torque = FR


The Attempt at a Solution



First I attempt to sort out the torques to see what cancels what. Since the wire loops are suppose to stay parallel to the magnetic field, the sum of the torques should be zero. Another thing to note is that the magnetic field only acts on the wire where they go perpendicular to the field. Since there are 10 loops here, that means that we have 10 times the force on each side of the wire loop (F = 10ILxB). So

mgr-10ILBr-10ILBr=0
mgr-20ILBR=0
mg=20ILB
(mg)/(20IL) = B

(.05*9.8)/(20*2*.1) = .1225 Tesla

Does this seem right?

Thanks!
 

Attachments

  • 33.P66.jpg
    33.P66.jpg
    6.5 KB · Views: 1,493
Physics news on Phys.org
Never freaking mind. An hour later and nothing posted. I got it right anyway.
 
Then post what you did to get it right.

EDIT: Oh whoops. Nevermind. Your original post is 100% correct. I just screwed up my calculation.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Derivation Of Torque On Current Loop Due To Uniform Magnetic Field
Replies
4
Views
2K
Understanding Torque in a Magnetic Field with Loop
Replies
37
Views
4K
Calculation of torque and force on magnetic dipole near infinite wire
Replies
3
Views
1K
How Do You Calculate the Magnetic Moment and Torque of a Rectangular Loop?
Replies
3
Views
3K
Understanding work in translation and rotation of a magnetic dipole
Replies
1
Views
2K
Effect of different magnetic fields on a magnetic dipole
Replies
25
Views
1K
Torque on a current loop caused by a magnetic field
Replies
5
Views
2K
Forces of a straight wire on a semi-circular wire loop (Magnetism)
Replies
17
Views
3K
Torque on a rectangular coil in a uniform magnetic field
Replies
7
Views
3K
Square copper wire loop within a magnetic field
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top