Solve U1=U*R2/(R1+R2): Current Circuit Theory

[Lindsayyyy]

Homework Statement

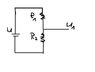
I want so show that U1=U*R2/(R1+R2) (sorry latex didn't work for me right now, don't know why)

Homework Equations

The Attempt at a Solution

I know the solution but I don't understand one step:
The solution says the following: the fall of voltage at U1 = R2*I (I is the current which comes from U). Why is that? Thats doesn't make sense to me, because I thought the current "splits" at this spot so I have: I=I1+I2.
Why does the solution say it's U=R2*I


Thanks for the help

 

[jeannagui]

well u is the emf of the source right ?
but what is this ---------u1 ? wat's U1

 

[Lindsayyyy]

I don't know how to describe it properly in english, but I think it's the voltage which drains off. I think the english term is voltage divider. But as I'am writing this I think I oversaw something.
The resistances are in series so the current is everywhere the same. Is this the right solution for the problem?

 

[I like Serena]

That's because the current does not really split.
The point where U1 is measured is not attached to anything, so no current flows.

This is indeed *only* a voltage divider.
Of course, when something (significant) is attached, the currents and voltages will change.

 

[Lindsayyyy]

Ok, I didn't recognize that I have to handle it this way. Thanks for the help