Engineering Solving a Circuit with a Complex Source

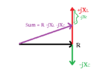
[Schfra]

Homework Statement

An image of the problem is attached. I need to solve for ic(t) and vc(t) by adding a complex source.

Homework Equations

The Attempt at a Solution

I don’t know where to start here. I don’t understand the question, and I can’t find the information I need in my notes. Can somebody explain what ic(t) and vc(t) are and what it means to add a complex source?

 

[gneill]

$i_c(t)$ is the circuit current in the time domain. $v_c(t)$ is the potential across the capacitor in the time domain.

To solve the problem in the easiest way you'll want to work in the frequency domain, i.e., with phasors. So you need to examine the expression that defines the voltage source and create a phasor (complex) representation of it. Convert the capacitance to its complex impedance. Analyze the circuit.

Once you have solutions in the frequency domain you can convert them to the time domain to answer parts (a) and (b).

 

[Schfra]

$i_c(t)$ is the circuit current in the time domain. $v_c(t)$ is the potential across the capacitor in the time domain.

To solve the problem in the easiest way you'll want to work in the frequency domain, i.e., with phasors. So you need to examine the expression that defines the voltage source and create a phasor (complex) representation of it. Convert the capacitance to its complex impedance. Analyze the circuit.

Once you have solutions in the frequency domain you can convert them to the time domain to answer parts (a) and (b).

I found the impedance of the capacitor to be .025j. I found the voltage to be 4.924-.868j. I then divided voltage by total resistance, and converted back to the time domain to get 5sin(20t+9.707deg) for ic(t).

Does this look correct so far?

 

[gneill]

Capacitors always have a negative impedance. Try again with $Z_C = -j0.025\; \Omega$.

 

[LvW]

Capacitors always have a negative impedance. Try again with $Z_C = -j0.025\; \Omega$.

Negative? Between voltage across and current through the capacitor there will be a phase difference of 90 deg.
Of course, we have 1/(jwC)=-jwC.
But are we allowed to say that the impedance is negative?
To me, this is not an academic discussion because in electronics we have "negative impedances" (negative and real)

 

[gneill]

Negative? Between voltage across and current through the capacitor there will be a phase difference of 90 deg.
Of course, we have 1/(jwC)=-jwC.
But are we allowed to say that the impedance is negative?
To me, this is not an academic discussion because in electronics we have "negative impedances" (negative and real)

Well, I was referring to the sign attributed to the quantity. Perhaps I was being a bit sloppy in my terminology when talking about an imaginary quantity.

 

[jim hardy]

But are we allowed to say that the impedance is negative?
To me, this is not an academic discussion because in electronics we have "negative impedances" (negative and real)

I was taught when starting out with complex arithmetic to always make a sketch
actually two or three sketches
one for the voltages, one for the impedances, and one for the currents.

e.g.

helps keep one's thinking straight
of course that was in the days of slide rules when it was vital to think one step at a time...

old jim

 

[Babadag]

As usually, I am late [very late it is now!].
I think it will be easier taken U as reference U[complex]=U+0i and Z=R-0.025i then I=U/Z.
For energy [reactive energy?]
En=∫(U/Z)^2*Xcdt and knowing that theoretically ∫f(t)^2*Xcdt|t=0 t=0.01|=f(t)^3/3/(df(x)/dt)|t=0 t=0.01 sec| you will find
En=2.22209E-06 VARsec?