PhoenixWright
- 20
- 1
Hello.
I have the following exercise, and I would like you to say to me if I have it right and how to proceed:
"A particle P moves with constant speed v along the X axis of a reference system O, being x0 = 0 the position in t = 0. Describe the movement on another system O' with the same origin of coordinates and rotating with angular velocity constant ω in the sense clockwise."
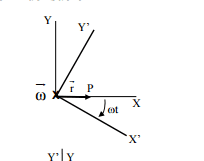
I have tried to solve as follows:
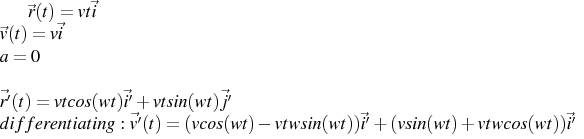
So far, is my point correct?
Now, I had thought find the acceleration:
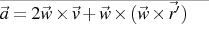
Is it correct?
Thank you!
I have the following exercise, and I would like you to say to me if I have it right and how to proceed:
"A particle P moves with constant speed v along the X axis of a reference system O, being x0 = 0 the position in t = 0. Describe the movement on another system O' with the same origin of coordinates and rotating with angular velocity constant ω in the sense clockwise."
I have tried to solve as follows:
So far, is my point correct?
Now, I had thought find the acceleration:
Is it correct?
Thank you!