Solving Charge Across Plates of a Capacitor w/ Negative Ions

[iVenky]

Homework Statement

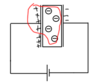
I have a material placed between parallel plates depleted of free electrons and contain negative ions. What would happen to the charge stored across the plates? Would it still be similar to placing a capacitor with a di-electric constant between them?

Homework Equations

Q=CV

The Attempt at a Solution

I am confused here because if I look at it in terms of E field, then the E field due to + charge on the plate and -ve ions cancel out at the other end of the plates. This means there would be unequal positive and negative charges on the parallel plates, which I am not sure makes sense.

Can you help me solve this question?

 

[Unconscious]

Would it still be similar to placing a capacitor with a di-electric constant between them?

It's a bit different.

What would happen to the charge stored across the plates?

Try calculating yourself using two times Gauss Law for charge on two 'good' surfaces.
With my calculations, if I didn't make mistakes, I obtained:

$$Q^{(\text{plate})}=\frac{\Delta V\cdot \epsilon \cdot A}{l}-\frac{\rho_{\text{ions}}\cdot l \cdot A }{2}$$

with obvious notation.

 

[iVenky]

It's a bit different.Try calculating yourself using two times Gauss Law for charge on two 'good' surfaces.
With my calculations, if I didn't make mistakes, I obtained:

$$Q^{(\text{plate})}=\frac{\Delta V\cdot \epsilon \cdot A}{l}-\frac{\rho_{\text{ions}}\cdot l \cdot A }{2}$$

with obvious notation.

If there is no supply (or voltage=0), you mean to say there would still be some charge on the plates (though the plates are neutral to begin with)?