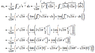UMich1344
- 26
- 0
Homework Statement
Calculate \frac{1}{\sqrt{2\pi}}\int^{\infty}_{-\infty}x^{2}e^{-\frac{x^{2}}{2}}dx
Use the fact that \int^{\infty}_{-\infty}e^{-\frac{x^{2}}{2}}dx=\sqrt{2\pi}
Homework Equations
I'm assuming that integration by parts is the best way to solve this.
http://www.math.hmc.edu/calculus/tutorials/int_by_parts/"
The Attempt at a Solution
I want to use integration by parts in order to solve this. I've attempted both combinations of u and v'. However, I'm not able to get an integral in any of my solutions that looks like the one above that is set equal to \sqrt{2\pi}.
I have plugged the equation into Mathematica and the answer comes out to be 1. However, getting my work to back that up is proving to be difficult.
Is integration by parts the right way to go about solving this one? Any help is greatly appreciated.
Last edited by a moderator: