You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Solving Inclined Pully Table: Acceleration & Tension
AI Thread Summary
To solve the inclined pulley problem involving two blocks with different masses, the coefficient of kinetic friction is used to calculate tension and acceleration, assuming the blocks are in motion. The total tension in the string is derived from the forces acting on each block, considering both gravitational force and friction. It is emphasized that tension remains constant throughout the string, but the forces acting on each mass must be analyzed separately to determine the net force and resulting acceleration. The discussion highlights the importance of drawing free body diagrams and applying Newton's second law to derive the correct equations. Understanding the relationship between mass, tension, and acceleration is crucial for solving such pulley problems effectively.
Physics news on Phys.org
danielu13
- 67
- 0
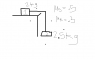
lames said:Homework Statement
block1 2kg
block2 2.5kg
coefficient of static friction =.5
coefficient of kinetic friction= .3
A)how can you find the acceleration and tension?
which coefficient do you use?
For the Tension, you calculate the amount of tension in each section of string and add them together. The tension in T1 is calculated by the force of friction with is
F_{friction} = F_N\mu_k
For this, you use the coefficient of kinetic friction, as I am assuming that the force is being calculated when the blocks are already moving.
So,
T = T_1 + T_2
T_1 = F_N\mu_k
T_1 = 5.886 N
T_2 = mg
T_2 = 24.525 N
T = 30.411 N
For the acceleration you use Newton's Second:
\Sigma\vec{F} = m\vec{a}
The sum of the forces in the system that we are looking at is contained within the tension of the wires, so
30.411 N = (4.5 kg)a
a = 6.758 \frac{m}{s^2}
lames
- 6
- 0
danielu13 said:For the Tension, you calculate the amount of tension in each section of string and add them together. The tension in T1 is calculated by the force of friction with is
F_{friction} = F_N\mu_k
For this, you use the coefficient of kinetic friction, as I am assuming that the force is being calculated when the blocks are already moving.
So,
T = T_1 + T_2
T_1 = F_N\mu_k
T_1 = 5.886 N
T_2 = mg
T_2 = 24.525 N
T = 30.411 N
For the acceleration you use Newton's Second:
\Sigma\vec{F} = m\vec{a}
The sum of the forces in the system that we are looking at is contained within the tension of the wires, so
30.411 N = (4.5 kg)a
a = 6.758 \frac{m}{s^2}
are you sure those are the right answers? did you look at the picture?
- 42,640
- 10,429
I disagree entirely with danielu3's analysis and answers.lames said:are you sure those are the right answers? did you look at the picture?
Since the (presumed) pulley is massless, the tension, T, is the same throughout the string.
The first thing, strictly speaking, is to check that the masses will move. Will the tension overcome the static friction?
Assuming so, the two masses each undergo the same acceleration, a.
Write down the forces on each mass. What net force is required in each case to produce the acceleration a? What two equations does that give you?
danielu13
- 67
- 0
Yes, the tension in the string is constant. However, there are two components to the tension in the string; one is caused by the force of gravity acting on mass 2 and the other is the force of friction acting on mass 1. I may have issues where I used a positive instead of negative. Tension is one of the things that has always caused me issues though.
- 42,640
- 10,429
You can't add tensions like that. Consider two equal masses, m, hung over a light pulley by a string. The tension in the string is mg, not 2mg. Now make the masses unequal. What is the tension now?danielu13 said:Yes, the tension in the string is constant. However, there are two components to the tension in the string; one is caused by the force of gravity acting on mass 2 and the other is the force of friction acting on mass 1.
danielu13
- 67
- 0
These pulley problems have always confused me for some reason. If there were two unequal masses on a pulley would the tension be
T = g\frac{m_1+m_2}{2}
?
T = g\frac{m_1+m_2}{2}
?
- 42,640
- 10,429
Don't just guess, try to reason it out. Think about the acceleration.danielu13 said:If there were two unequal masses on a pulley would the tension be
T = g\frac{m_1+m_2}{2}
danielu13
- 67
- 0
Well, based on what you said, I was thinking that the tension is based on the even distribution of the masses, which is why I'm thinking the average of the masses. But I have some feeling that it should be g(m2-m1) since the pulley makes the gravitational forces counteract each other. Am I at least thinking in the right direction right now?
- 42,640
- 10,429
Let the acceleration be a (down for the heavier, up for the lighter) and the tension be T.danielu13 said:Well, based on what you said, I was thinking that the tension is based on the even distribution of the masses, which is why I'm thinking the average of the masses. But I have some feeling that it should be g(m2-m1) since the pulley makes the gravitational forces counteract each other. Am I at least thinking in the right direction right now?
Draw a free body diagram for each mass and write out the F=ma equation for each.
Similar threads
- Replies
- 10
- Views
- 2K
- Replies
- 13
- Views
- 3K
- Replies
- 16
- Views
- 5K
- Replies
- 7
- Views
- 4K
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 3K
- Replies
- 5
- Views
- 2K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math