wazzup
- 12
- 0
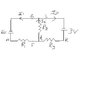
Q) Given R1=10 Ohms, R2=15 Ohms, R3=5 Ohms, find the current going through each resistor in this pathway in the attached circuit diagram.
My solution is as follows.. i'd appreciate it if you guys could verify if its correct or not:
I2=I1+I3-------------------------Equation 1
Starting from a and going through loop agdf:
-E1+I2R2+I1R1=0
15I2+10I1=6 -----------------Equation 2
Starting from k and going through loop kmdl:
-I3R3-I2R2+E2=0
-5I3-15I2=-3--------------------Equation 3
Plugging Equation 1 into Equation 2
15I2+10(I2-I3)=6
25I2-10I3=6--------------------Equation 4
Adding Equation 3 and Equation 4
25I2 - 10I3= 6
-15I2 - 5I3=-3
By multiplying equation 4 by 2 and then subtracting both, I get:
55I2=12
I2= .218A
Plugging this value of I2 into Equation 4:
25I2-10I3=6
25(.218) - 10I3=6
-10I3=.55
I3= -0.055A
Plugging I2 and I3 into Equation 1
I2=I1+I3
I1=I2-I3
I1= (.218A)-(-0.055A) = .273A
Therefore, I1= 0.273A
I2= 0.218A
I3= -0.055A
Thanks much.
My solution is as follows.. i'd appreciate it if you guys could verify if its correct or not:
I2=I1+I3-------------------------Equation 1
Starting from a and going through loop agdf:
-E1+I2R2+I1R1=0
15I2+10I1=6 -----------------Equation 2
Starting from k and going through loop kmdl:
-I3R3-I2R2+E2=0
-5I3-15I2=-3--------------------Equation 3
Plugging Equation 1 into Equation 2
15I2+10(I2-I3)=6
25I2-10I3=6--------------------Equation 4
Adding Equation 3 and Equation 4
25I2 - 10I3= 6
-15I2 - 5I3=-3
By multiplying equation 4 by 2 and then subtracting both, I get:
55I2=12
I2= .218A
Plugging this value of I2 into Equation 4:
25I2-10I3=6
25(.218) - 10I3=6
-10I3=.55
I3= -0.055A
Plugging I2 and I3 into Equation 1
I2=I1+I3
I1=I2-I3
I1= (.218A)-(-0.055A) = .273A
Therefore, I1= 0.273A
I2= 0.218A
I3= -0.055A
Thanks much.