Solving Max Volume Right Circular Cone Inscribed in Sphere Radius 3cm

[PhysicsinCalifornia]

HW problem--NEED HELP!

This is an optimization problem with differential calc. I really need help with this

Here's the prob:

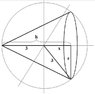
A right circular cone is being inscribed in a sphere of radius 3cm.

Find
a) the dimensions (base radius, and height) of the right circular cone with the largest volume
b) the cone's volume

Here's what I got::

Volume for sphere is
$$V_s = \frac{4}{3}\pi r^3$$
and the volume for the cone is
$$V_c = \frac{1}{3}\pi r^2 h$$
(obviously)

Now i got that $$h = 3+x$$
*Note that I cannot draw a pic, so it's hard to describe

Also, $$x = \sqrt{9 - r^2}$$ using pythagorean's theorem

so the height would equal the radius of the sphere, 3 cm, plus x

Therefore
$$V(r) = \frac{1}{3} \pi r^2 (3 + \sqrt{9- r^2}) = \pi r^2 + \frac{\pi r^2 \sqrt{9 - r^2}}{3}$$

leaving everything in terms of r because we want the largest volume

How do I work it from here?

Thanks for your help in advance

 

[tiagobt]

I guess you're right so far. You should try to calculate $$V'(r)$$ now. After that, you'll need to solve $$V'(r) = 0$$ in order to find the critical points of the function. One of them should be the maximum point. In order to differentiate the function, you'll need to use the multiplication rule in the second term.

 

[OlderDan]

I guess you're right so far. You should try to calculate $$V'(r)$$ now. After that, you'll need to solve $$V'(r) = 0$$ in order to find the critical points of the function. One of them should be the maximum point. To derive the function, you'll need to use the multiplication rule in the second term.

Wow! How did this problem go undetected for a couple of days? Good for you for digging back far enough to find it. I was at first bothered by the use of r twice to mean different things in the original equations,

$$V_s = \frac{4}{3}\pi r^3$$

$$V_c = \frac{1}{3}\pi r^2 h$$

but since the first one is a constant r = 3 and is used correctly in the formulation of the volume of the cone, it is not a problem. I drew a diagram for myself, so I'll pass it along.

An observation about your reply- The verb "derive" in your statement "To derive the function, you'll need to use the multiplication rule in the second term" should be "differentiate". Derive does not mean to take the derivative of. In mathematics it means "To arrive at by reasoning; deduce or infer: derive a conclusion from facts"

 

[tiagobt]

Wow! How did this problem go undetected for a couple of days? Good for you for digging back far enough to find it. I was at first bothered by the use of r twice to mean different things in the original equations,

$$V_s = \frac{4}{3}\pi r^3$$

$$V_c = \frac{1}{3}\pi r^2 h$$

but since the first one is a constant r = 3 and is used correctly in the formulation of the volume of the cone, it is not a problem. I drew a diagram for myself, so I'll pass it along.

An observation about your reply- The verb "derive" in your statement "To derive the function, you'll need to use the multiplication rule in the second term" should be "differentiate". Derive does not mean to take the derivative of. In mathematics it means "To arrive at by reasoning; deduce or infer: derive a conclusion from facts"

Yes, at first I was bothered with the use of the letter $$r$$ for two different things too. But PhysicsinCalifornia didn't mess things up. I'm sorry for the misuse of the word "derive". English is not my mother language and sometimes I say things that sound weird... I'm going to edit my reply though.

Tiago