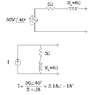
The discussion focuses on finding tutorials for solving network nodal voltages and converting voltage sources to current sources, specifically using Norton's theorem. Participants clarify that a voltage source in series with a resistor can be transformed into a current source in parallel with the same resistor. There is confusion regarding the conversion of complex numbers from Cartesian to polar form, with explanations provided about using Euler's formula and calculating angles using the arctangent function. The correct method for evaluating current using the given voltage and impedance is also discussed, leading to a clearer understanding of phasor notation. Overall, the conversation emphasizes the importance of mastering these concepts for effective circuit analysis.