Raihan
- 19
- 0
Please help me to solve this RLC circuit problem. I am completely confused.If you give me the direct answer it would be much appreciated.
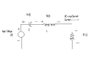
For the series RLC circuit in Figure, find the input/output
difference equation for
1.y(t)=v_{R}
2.Y(t)=i(t)
3.y(t)=v_{L}
4.y(t)=v_{C}
I have attached the Circuit diagram in a .jpg file.
For the series RLC circuit in Figure, find the input/output
difference equation for
1.y(t)=v_{R}
2.Y(t)=i(t)
3.y(t)=v_{L}
4.y(t)=v_{C}
I have attached the Circuit diagram in a .jpg file.
Attachments
Last edited by a moderator: