- #1
Lone Wolf
- 10
- 1
- Homework Statement
- A small sphere of radius r = 5 cm, with mass = 50 g, is dropped from rest from the top of a ramp with height = 0.73 m, as show in the figure. The moment of inertia of a sphere about its center is I = 2/5 MR². Consider g = 10 m/s².
a) Considering a sphere that rolls without slipping, find the speed of the sphere at point A (0.1 m above the base of the ramp).
b) Find the maximum height h, reached by the sphere.
c) Considering the sphere now only slips (does not roll), determine whether the maximum height will be greater or less than the previous case, without doing any calculations.
- Relevant Equations
- Conservation of mechanical energy: ΔEm = 0.
Kinetic energy for a rolling object: 1/2 * I * ω² + 1/2 * m * v² , where v is the velocity of the center of mass.
Potential energy = m * g * h, where h is the height of the center of mass.
Figure:
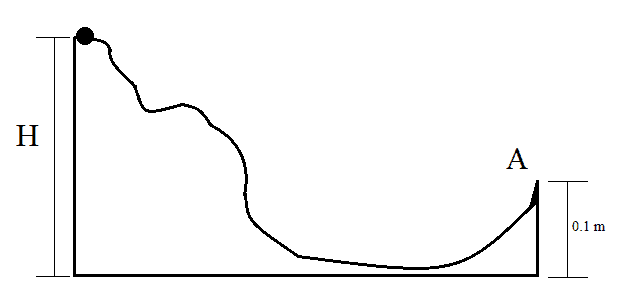
a)
The mechanical energy of the sphere is conserved because the weight is the only force which does work. My problem with this question is mostly because the original picture (which I tried to recreate here) is kind of ambiguous, as in I don't know if H already accounts for the radius of the sphere or not.
Initial potential energy: m * g * hi = 0.05 * 10 * 0.73 = 0.365 J.
Final potential energy: m * g * hf = 0.05 * 10 * (0.1) = 0.05 J.
Initial kinetic energy = 0 J
Final kinetic energy = 1/2 * I * ω² + 1/2 * m * v²; for an object that rolls without slipping, ω = v/R.
Kf = (7 * m * v²)/10 = 0.035 * v²
K(initial) + Ep(initial) = Ep(final) + K(final)
0.365 = 0.05 + 0.035v² ---> v = 3 m/s.
b)
Since the question does not mention any air resistance, the conservation of mechanical energy is still applicable. So the height of the sphere will be the same as it was initially (H = 0.73 m).
c) In order for an object to roll without slipping, there must be a friction force. So considering the ramp is not frictionless, as the sphere slides without rolling, it loses mechanical energy due to work done by the friction force, at point A the speed will be less than the one calculated for a), and therefore the sphere will reach a smaller height than 0.73 m.
I am not sure if the work I've done is correct. Any confirmations/corrections are appreciated.
a)
The mechanical energy of the sphere is conserved because the weight is the only force which does work. My problem with this question is mostly because the original picture (which I tried to recreate here) is kind of ambiguous, as in I don't know if H already accounts for the radius of the sphere or not.
Initial potential energy: m * g * hi = 0.05 * 10 * 0.73 = 0.365 J.
Final potential energy: m * g * hf = 0.05 * 10 * (0.1) = 0.05 J.
Initial kinetic energy = 0 J
Final kinetic energy = 1/2 * I * ω² + 1/2 * m * v²; for an object that rolls without slipping, ω = v/R.
Kf = (7 * m * v²)/10 = 0.035 * v²
K(initial) + Ep(initial) = Ep(final) + K(final)
0.365 = 0.05 + 0.035v² ---> v = 3 m/s.
b)
Since the question does not mention any air resistance, the conservation of mechanical energy is still applicable. So the height of the sphere will be the same as it was initially (H = 0.73 m).
c) In order for an object to roll without slipping, there must be a friction force. So considering the ramp is not frictionless, as the sphere slides without rolling, it loses mechanical energy due to work done by the friction force, at point A the speed will be less than the one calculated for a), and therefore the sphere will reach a smaller height than 0.73 m.
I am not sure if the work I've done is correct. Any confirmations/corrections are appreciated.