PhMichael
- 134
- 0
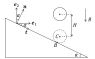
The sphere is released at a height [itex]H[/itex] above a fixed inclined plane, as shown in the attached figure.
The coefficient of restitution at impact is [itex]e>0[/itex] (that is the sphere leaves the surface just after impact), the coefficient of friction between the sphere and the plane is [itex]\mu[/itex].
I need a clarification to what happens during impact.
Is it even possible for the sphere to roll without slipping during the very short time interval of impact with the inclined plane?
I would assume that since the velocity component in the tangent direction [itex]\boldsymbol{t}[/itex] of the impact point on the sphere (B) just before impact is nonzero, specifically it equals [itex]\sqrt{2gH} \sin(\alpha)[/itex], the sphere would necessarily slip on the inclined plane with the impulsive friction force pointing in the negative [itex]\boldsymbol{t}[/itex] direction and having the magnitude [itex]|\hat{f}| = \mu |\hat{N}|[/itex] (a superposed hat denotes an impulse).
Using the balance equations of linear and angular impulse-momentum together with the definition of the coefficient of restitution, it is possible to obtain the velocity of the center of mass of the sphere and its angular velocity. However, if a no-slip condition during impact is imposed, then there is another constraint on the velocity of the impact point (B) on the sphere, which, in my opinion, is not a possible scenario. Am I right?
The coefficient of restitution at impact is [itex]e>0[/itex] (that is the sphere leaves the surface just after impact), the coefficient of friction between the sphere and the plane is [itex]\mu[/itex].
I need a clarification to what happens during impact.
Is it even possible for the sphere to roll without slipping during the very short time interval of impact with the inclined plane?
I would assume that since the velocity component in the tangent direction [itex]\boldsymbol{t}[/itex] of the impact point on the sphere (B) just before impact is nonzero, specifically it equals [itex]\sqrt{2gH} \sin(\alpha)[/itex], the sphere would necessarily slip on the inclined plane with the impulsive friction force pointing in the negative [itex]\boldsymbol{t}[/itex] direction and having the magnitude [itex]|\hat{f}| = \mu |\hat{N}|[/itex] (a superposed hat denotes an impulse).
Using the balance equations of linear and angular impulse-momentum together with the definition of the coefficient of restitution, it is possible to obtain the velocity of the center of mass of the sphere and its angular velocity. However, if a no-slip condition during impact is imposed, then there is another constraint on the velocity of the impact point (B) on the sphere, which, in my opinion, is not a possible scenario. Am I right?
