mitleid
- 56
- 1
A spherical capacitor is made of two insulating spherical shells with different dielectric strengths, k1 and k2, situated between two spherical metallic shells and separated by a vacuum gap. Calculate the capacitance of this system.
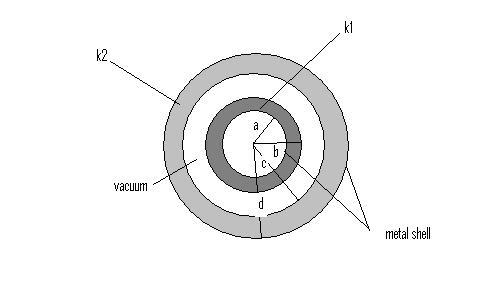
Total C = Q(free) / \DeltaV where \LambdaV is the varied potential between the two metal shells.
\LambdaV = \int^{a}_{d}E(r)dr = - \int^{a}_{b}[(1/4*pi*Eps) * (1/k1)*(Qfree / r^2) * dr] - \int^{b}_{c}[(1/4*pi*Eps) * (Qfree / r^2) * dr] - \int^{c}_{d}[(1/4*pi*Eps) * (1/k2) * (Qfree / r^2) * dr]
Q free will be negated in the final equation, since C = Q/V and V includes Q in its numerator (hope that makes sense). So after integrating V through each of the mediums, the two dielectrics and the vacuum, I get the sum :
Ctotal = = Ke[C(dielectric 1) + C(vacuum) + C(dielectric 2) = Ke[(1/k1)*(1/a - 1/b) + (1/b - 1/c) + (1/k2)*(1/c - 1/d)]
Is this correct?
Total C = Q(free) / \DeltaV where \LambdaV is the varied potential between the two metal shells.
\LambdaV = \int^{a}_{d}E(r)dr = - \int^{a}_{b}[(1/4*pi*Eps) * (1/k1)*(Qfree / r^2) * dr] - \int^{b}_{c}[(1/4*pi*Eps) * (Qfree / r^2) * dr] - \int^{c}_{d}[(1/4*pi*Eps) * (1/k2) * (Qfree / r^2) * dr]
Q free will be negated in the final equation, since C = Q/V and V includes Q in its numerator (hope that makes sense). So after integrating V through each of the mediums, the two dielectrics and the vacuum, I get the sum :
Ctotal = = Ke[C(dielectric 1) + C(vacuum) + C(dielectric 2) = Ke[(1/k1)*(1/a - 1/b) + (1/b - 1/c) + (1/k2)*(1/c - 1/d)]
Is this correct?