ANKIT SAJWAN
Homework Statement
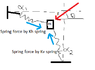
Two linear springs with stiffness Kh, Kv are attached to a single mass m at right angle to each other, i.e; one of the spring(Kh) is in the horizontal direction(x-axis) and the other(Kv) is in the vertical direction(y-axis).
A constant force F is being applied to the mass, inclined at an angle theta with the x-axis.
I need to find the angle which the springs Kh, Kv will subtend with the x-axis and y-axis respectively at the postion of static equilibrium.
Homework Equations
F = K * x
The Attempt at a Solution
I attempted the problem by assuming that the horizontal component of F will just compress the Kh spring by some distance, say a , while the Kv spring will not have any effect as the force is perpendicular to the linear spring. Did the similar thing for vertical component of F.
My query is, is it correct to assume that the horizontal component of F will not have any effect on Kv, as from geometry we can see that if the spring Kh moves by distance a, then the spring Kv will elongate.