Spring forces / Deflection of springs of members

[RelicJ]

Homework Statement

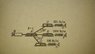
The brake linkage for a truck is actuated by hydraulic cylinder AB. Cylinder AB, springs CD, EF, and GH are the slotted tracks are all horizontal. The slotted tracks are frictionless. If the cylinder AB exerts a tensile force of 12 kips, determine the deflection d and the forces in members AC, AE, and AG.

The photograph of the situation given is below, along with my attempt with free body diagrams.

Homework Equations

F = kd (spring equation)

The Attempt at a Solution

I was unsure where to really start, but my teacher did give us a few clues. I broke the problem into 4 different free body diagrams which I have attached and I figured out multiple equations using equilibrium equations like sums of forces in the x and y direction. I am unsure where to go from here... if this is even correct.

 

[CWatters]

Once the brakes are operated and everything has stopped moving the forces on various points sum to zero. For example on point G in the horizontal direction you can write..

F_AGCos(45) + F_GH = 0

You can write other similar equations for other points in your diagrams including one for point A.

You also know that points CE and G all move the same distance.

Should be possible to write enough equations to solve for the unknowns.