How to Solve a Spring and Pulley Problem with a 3.8-kg Sphere?

[MG5]

A 3.8-kg sphere is suspended by a cord that passes over a 1.3-kg pulley of radius 3.5 cm. The cord is attached to a spring whose force constant is k = 86 N/m as in the figure below. Assume the pulley is a solid disk.

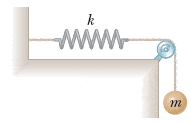
(a) If the sphere is released from rest with the spring unstretched, what distance does the sphere fall through before stopping?

The answer to this is .866 m. Not sure how to get it though.

(b) Find the speed of the sphere after it has fallen 25 cm.

Answer to this is 1.73 m/s. Not sure how to get this either.

I'm not quite sure how to start this. I guess I'd use...

1/2kx² for the spring, mgh since the sphere has PE before falling, 1/2mv² for final KE of the falling sphere. And I'd have to do something about the pulley. I guess KE=Iω² since its rotating? Not sure about that. And its a sphere that is falling and the I for a sphere is I=2/5mr². Dont know if that's needed for this problem. Any help would be great. Thanks.

 

[tiny-tim]

Hi MG5!

(a) If the sphere is released from rest with the spring unstretched, what distance does the sphere fall through before stopping?

The answer to this is .866 m. Not sure how to get it though.

same method you're using for (b), with final speed 0 for both the sphere and the pulley

(b) Find the speed of the sphere after it has fallen 25 cm.

Answer to this is 1.73 m/s. Not sure how to get this either.

I'm not quite sure how to start this. I guess I'd use...

1/2kx² for the spring, mgh since the sphere has PE before falling, 1/2mv² for final KE of the falling sphere. And I'd have to do something about the pulley. I guess KE=Iω² since its rotating?

1/2 Iω², otherwise yes

And its a sphere that is falling and the I for a sphere is I=2/5mr². Dont know if that's needed for this problem.

no, you only need moment of inertia if the sphere is rotating

 

[MG5]

Hi MG5!


same method you're using for (b), with final speed 0 for both the sphere and the pulley


1/2 Iω², otherwise yes


no, you only need moment of inertia if the sphere is rotating

Yeah I meant to add the 1/2 in there. Thanks for pointing that out. I'm going to give it another shot and see how it goes.

 

[lewando]

For what its worth for (a), when the sphere loses the maximum PE, the spring will have gained maximum PE. Conveniently, at this time the pulley is not spinning. This does not help with (b) though.

 

[MG5]

Ok this is the equation I came up with. Doesnt seem right though.

mgh_i=1/2mv²+1/2kx²

I don't know what the height would be though

 

[tiny-tim]

is this (a) or (b)?

if it's (a), v = 0; if it's (b), what about ω ?

 

[lewando]

As long as the cord does not stretch x and h will be related.

 

[MG5]

is this (a) or (b)?

if it's (a), v = 0; if it's (b), what about ω ?

First I'm trying to figure out (a). Then I'll try to do (b)

Well the 1/2mv² was the final KE. If it was initial it would be zero. But yeah I just realized I don't have the velocity either. Too many unknowns

 

[tiny-tim]

Well the 1/2mv² was the final KE. If it was initial it would be zero. But yeah I just realized I don't have the velocity either. Too many unknowns

but the final velocity is also zero …

(a) …what distance does the sphere fall through before stopping?

 

[MG5]

but the final velocity is also zero …

yeah I saw that but I still wasnt sure.

So would it be something like mgh=1/2kx^2

 

[tiny-tim]

yeah I saw that but I still wasnt sure.

why??!

So would it be something like mgh=1/2kx^2

yup!

 

[MG5]

why??!


yup!

I thought it wasnt just because in like projectile motion problems when it asks how far something traveled and like where it hit the ground from its initial starting point the final velocity was never zero. I thought we usually needed that value to find x. But that's a completely different problem. Now I know.

Only problem with that equation is I have no idea what the height is to put into mgh.

 

[arildno]

Set up an energy equation.
Remember that mgh, FOR THE PULLEY,is a constant until "Dovre falls"
(Dovre is a mountain chain in my native country Norway!)

 

[tiny-tim]

Only problem with that equation is I have no idea what the height is to put into mgh.

same as x !

 

[MG5]

same as x !

but then there's two unknowns, one on each side of the equation. Sorry if I'm just really off with this. Hopefully you can bear with me.

 

[lewando]

but then there's two unknowns, one on each side of the equation. Sorry if I'm just really off with this. Hopefully you can bear with me.

No worries! x = h. x can be substituted for h and vice-versa. [edit-- sorry]

 

[MG5]

No worries! x = y. x can be substituted for y and vice-versa.

Yeah but still. It could be giraffe lol. Its still an unknown.

 

[lewando]

You have 2 equations and 2 unknowns.

kx²/2= mgh

x = h

This is solvable.

[edit-- I originally said x = y, I meant x = h]

 

[MG5]

You have 2 equations and 2 unknowns.

kx²/2= mgh

x = h

This is solvable.

Yeah it is. Sorry I'm just not used to having to unknowns. As usual, I was making it much harder than it was.

I got it

3.8kg(9.8)x=1/2(86N/m)x^2

37.24x=43x^3

Subtract 37.24, then do 43/37.24, and you get the answer .866. That was easy.

Now the second part.

Finding the speed after it has fallen .25 meters.

 

[lewando]

What?

3.8kg(9.8)x=1/2(86N/m)x^2

37.24x=43x^3

Subtract 37.24, then do 43/37.24, and you get the answer .866. That was easy.

There should be no subtraction and no x³.

Unless that's a typo, you got lucky on the math. Make sure you are clear on this before proceeding.

 

[MG5]

What?

There should be no subtraction and no x³.

Unless that's a typo, you got lucky on the math. Make sure you are clear on this before proceeding.

Yeah that was suppose to be x^2. and yeah I didnt subtract anything lol i don't know why I wrote that. I just ended up with 37.24=43x, divided, x =.866. I got it.

 

[lewando]

By now you should be thinking how to solve this with conservation of energy concepts. I need to clockout for the evening but I will leave you with this general outline:

When the system first begins, all the energy is in the sphere in the form of PE. Since PE is relative to some reference point, I suggest you use the result from (a) to serve as your maximum and minimum (zero) PE_sphere references.

As the system begins moving, PE_sphere is reduced, KE_sphere starts increasing, PE_spring starts increasing, and KE_pulley starts increasing.

As arildno suggested, set up an energy equation involving all these terms. Relate the terms that you do not know (KE_pulley, and KE_sphere) to v, which you will solve for.

 

[MG5]

By now you should be thinking how to solve this with conservation of energy concepts. I need to clockout for the evening but I will leave you with this general outline:

When the system first begins, all the energy is in the sphere in the form of PE. Since PE is relative to some reference point, I suggest you use the result from (a) to serve as your maximum and minimum (zero) PE_sphere references.

As the system begins moving, PE_sphere is reduced, KE_sphere starts increasing, PE_spring starts increasing, and KE_pulley starts increasing.

As arildno suggested, set up an energy equation involving all these terms. Relate the terms that you do not know (KE_pulley, and KE_sphere) to v, which you will solve for.

Ok so something like 1/2mv^2 + 1/2kx^2 = 1/2Iw^2. not quite though but yeah I've been trying to set up the conservation equation and cancelling out the things i don't need

 

[tiny-tim]

(just got up :zzz:)

but then there's two unknowns, one on each side of the equation. Sorry if I'm just really off with this. Hopefully you can bear with me.

show us what you've got