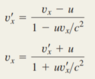rugerts
- 153
- 11
Homework Statement
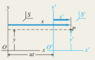
Two particles in a high-energy accelerator experiment approach each other head-on with a relative speed of 0.890c. Both particles travel at the same speed as measured in the laboratory. What is the speed of each particle, as measured in the laboratory?
Homework Equations
The Attempt at a Solution
I've interpreted the relative velocity between the two as 0.890c and the velocity of, say particle 2, to be -v wrt laboratory S and -v wrt S'. The answer appears to be 0.611c which is way off from what I've got.