winston
- 2
- 0
The figure below shows an electrostatic method of separating conducting and non-conducting spheres
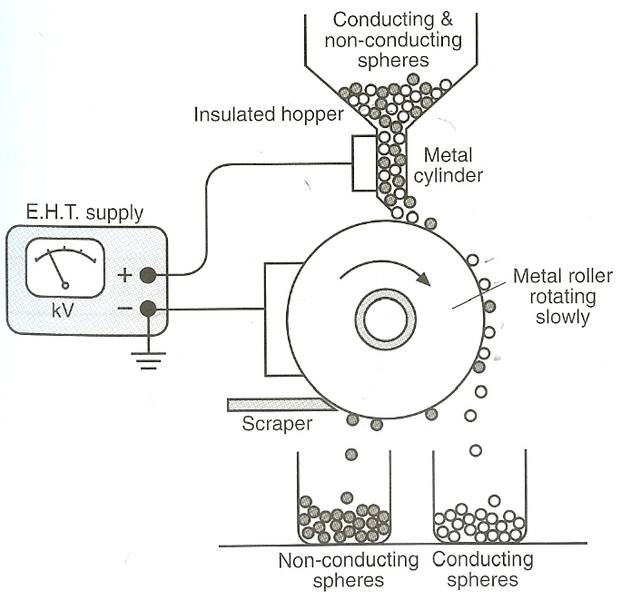
Why do the conducting spheres fall off from the roller while the non-conducting spheres have to be scrapped off?
Thanks for the help.
Cheers,
Winston
Why do the conducting spheres fall off from the roller while the non-conducting spheres have to be scrapped off?
Thanks for the help.
Cheers,
Winston