itsalwysunny
- 4
- 0
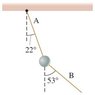
1. A 19.0 kg ball is supported from the ceiling by rope A. Rope B pulls downward and to the side on the ball. If the angle of A to the vertical is 22 degrees and if B makes an angle of 53 degrees to the vertical find the tension in rope A and then find the tension in rope B