suspenc3
- 400
- 0
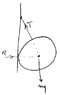
A uniform sphere of mass m and radius r is held in place by a massless rope attached to a frictionless wall a distance L above the Centre of the sphere. Find the tension in the rope and the force on the sphere from the wall.
I tried to get a picture, but it is apparently too big to host.
Do I start with a FBD? If so what should it look like?, How can I find T?
I tried to get a picture, but it is apparently too big to host.
Do I start with a FBD? If so what should it look like?, How can I find T?