psneath
- 3
- 0
Homework Statement
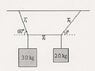
The attached system is in static equilibrium, and the string in the middle is exactly horizontal.
Find:
a)tension T1
b)tension T2
c)tension T3
d)angle theta
Homework Equations
I know I need to create equations that equal zero to analyze the x and y components of force as well as torque
The Attempt at a Solution
So
Fx=T3x-T1x=0 (I think the tension in T2 is zero)
Fy=T1y + T3y-m3g-m2g=0
For the torque equation I'm using the axis of rotation as the point where T1 meets m3
torque = T2R + T3yR - m2gR
When I try to solve any of these I come across way too many unknowns to solve...can someone see if I've assessed for forces properly and show me where to go from here?
Thanks!