anne921
- 10
- 0
Homework Statement
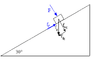
The coefficient of static friction between the box (6.75 kg) and the ramp (30 degree incline) is 0.500. What is the magnitude of the minimum force, F, that must be applied to the box perpendicularly to the ramp to prevent the box from sliding?
Homework Equations
The Attempt at a Solution
The key says the answer to this question is 124N but I am unable to reach that answer. I think I am missing something and/or using the wrong equation. Please help me!