equinom
- 3
- 0
The problem is: Two blocks of mass m and M are connected via pulley with a configuration as shown. The coefficient of static friction is 0.64, between blocks and surface. If the inclined angle is 23deg and M = 3.1kg, what is the maximum mass m so that no sliding occurs?
The question is: I understand how m=0.64(3.1)/(sin23-0.64cos23) but how can I explain the negative mass? Also, when you look at the denominator there is a restriction that theta can't equal 33 degrees. What exactly does that mean?
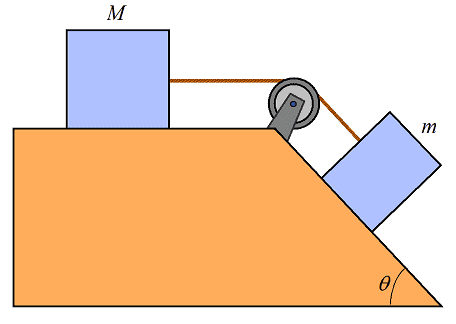
The question is: I understand how m=0.64(3.1)/(sin23-0.64cos23) but how can I explain the negative mass? Also, when you look at the denominator there is a restriction that theta can't equal 33 degrees. What exactly does that mean?