alexmath
- 35
- 0
Homework Statement
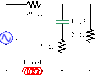
Hello everyone! I have the following circuit to solve, and my result is a bit wrong... can you tell me please where's the mistake?
E=10sin(1000t)
Find the current delivered to the circuit. Find the equivalent impedance of the circuit. Find the equation of the current and voltage drop for each element of the circuit.
Homework Equations
I tried first to solve for the equivalent impedance.
Vrms=10/√2
Xc= -j * 1/wc
Xl = jwl
w=1000 rad/s
The Attempt at a Solution
R1=100Ω, R2=20Ω, R3=50Ω, Xc=-100j, Xl=40j
therefore equivalent impedance is: 100+40j+ ((1/(50-100j))+0.05)^(-1)=40j+100, in polar form: 107.7 < 21.8, so the impedance=107.7/√2(1000t+ 21.8°)Ω.
Is that correct?
Attachments
Last edited: