- #1
Tanya Sharma
- 1,540
- 135
Homework Statement
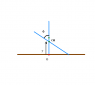
A stick of mass M and length L is held vertically on a frictionless surface. A gentle push at the top causes the rod to fall from this position . Find the speed of its center of mass when it makes an angle θ with vertical .
a) Use force method
b) Use energy method
Homework Equations
F=Ma
τ=Iα
The Attempt at a Solution
First I tried using the Newtons laws of translation and rotation .
1) The forces acting in the vertical direction are Mg and Normal from the floor at the lower end (N) .
$$ Mg - N = Ma_{cm} $$
2) Writing torque equation about CM ,
$$ N\frac{L}{2}sinθ = \frac{ML^2}{12}\ddotθ $$
3) ycm = (L/2)cosθ
So , $$ v_{cm} = -\frac{L}{2}(\dotθsinθ) $$
and , $$ a_{cm} = -\frac{L}{2}[\ddotθsinθ + (\dotθ^2)cosθ] $$
Using the above three equations,I end up with
$$ a_{cm} = \frac{1}{1-3sin^2θ}(-3gsin^2θ - \frac{L}{2}\dotθ^2cosθ ) $$
But I need to find relation between vcm and θ .
I would be grateful if somebody could help me with the problem .
Last edited: