- #1
guideonl
- 58
- 6
Hi everyone,
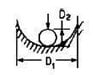
What is the area should be taken to determine the compression stress of pin-hole in tention force (i.e plate with known thickness having a hole for lifting shakle pin) where the hole diameter is greater than the pin diameter (> x3) (theoretically, it is not an area just line of contact between the hole and the pin, which is the thickness of the plate).
Thank you, Guideon
What is the area should be taken to determine the compression stress of pin-hole in tention force (i.e plate with known thickness having a hole for lifting shakle pin) where the hole diameter is greater than the pin diameter (> x3) (theoretically, it is not an area just line of contact between the hole and the pin, which is the thickness of the plate).
Thank you, Guideon