RoKr93
- 21
- 0
Homework Statement
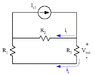
For the above circuit, find the coefficients of the linear relationship vout = a1vs1 + a2is2 + a3is3 by superposition. Then find the power delivered to R3 when vs1 = 100 V, is2 = 2 A, and is3 = 4 A. Given: R1 = 20 Ω, R2 = 60 Ω, and R3 = 20 Ω.
Homework Equations
Ohm's Law: V = IR
KVL: V1 + V2 + ... Vn = 0 for closed loops
KCL: I1 + I2 + ... In = 0 going in an out of a node
Voltage Division: V1 = Vsource * (R1/(R1+R2))
The Attempt at a Solution
I think I got the first two coefficients (though I could be incorrect). I found vout1 = vs1*(R3/(R1+R2+R3)) = 0.2Vs1 through voltage division. I'm pretty certain that's correct.
I also found that vout2 = Is2*R3 = 20Is2, though I'm not quite as certain about that.
But I absolutely cannot wrap my head around finding vout3 (when all independent sources are eliminated except Is3). I understand that in that situation, the Is2 branch essentially disappears and we are left with Is3 in parallel with a branch with R2 and a branch with R1 and R3, but we can't combine those since vout3 must stay isolated. I'm not sure what to do.