Calculating Drop Size, Number and Time for Water Flow Through Capillary

AI Thread Summary
The discussion revolves around calculating the radius of water droplets, the number of droplets from 10g of water, and the time required for the water to flow through a capillary tube. The user attempts to derive equations based on the balance of forces acting on a droplet at the end of the tube, incorporating parameters like surface tension and the density of water. The user expresses uncertainty about their approach and seeks validation of their calculations. There is a suggestion to consolidate thoughts into fewer posts to enhance clarity. The conversation emphasizes the need for a clear understanding of fluid dynamics principles in this context.
10bunny10
Messages
6
Reaction score
0

Homework Statement


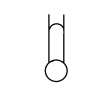
Trough a capillary with an inner radius r=1mm water flows in a form of small spherical droplets. What is the radius of the drops, the number of drops in m=10g water and the time needed the water to expire, if the surface tension of the water is =72x10^-3N/m, and the period between two drops is t=2s.


Homework Equations





The Attempt at a Solution


I need an idea how to imagine the situation and what to take into consideration? Help please :/
 
Physics news on Phys.org
I tried something:
When the drop is at the end of the tube just before to fall
αl1+αl2=m0g
where m0 is the mass of one drop
2απr+2απR=m0g
R=m0g2απr/2απ
V0=4R3π/3
m0=ρV0
m0=4ρR3π/3
N=m/m0
N=3m/4ρR3π
τ=t3m/4ρR3π
t=2s
 
Last edited:
Here is how I imagined it.
 

Attachments

  • kapka.png
    kapka.png
    562 bytes · Views: 450
Can anybody tell me if it is correct please?
 
You could've just used the edit button instead of posting 4 times on this thread that you pretty much just started.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Calculating Capillary Amount Given Aorta Blood Flow
Replies
1
Views
8K
How to Calculate the Length of a Capillary Tube for a Drip-Irrigation Emitter
Replies
3
Views
2K
How Does Water Flow Rate Change Over Time in a Draining Cylinder?
Replies
1
Views
2K
Water flowing through an eavestrough
Replies
6
Views
2K
Calculating Pressure Inside a Water Mist Droplet
Replies
3
Views
2K
How Does Bernoulli's Principle Apply to Varying Pipe Diameters and Water Flow?
Replies
3
Views
2K
Initial velocity and time of motion through water
Replies
2
Views
1K
Calculating Pump Power for Steady Water Flow: Work-Energy Theorem Approach
Replies
3
Views
7K
Time for a Droplet of Water to Fall .25m from Hole
Replies
3
Views
2K
Volume flow through a one side closed capillary
Replies
7
Views
3K

Hot Threads

Recent Insights

Back
Top