binbagsss
- 1,291
- 12
1. Homework Statement
Question attached.
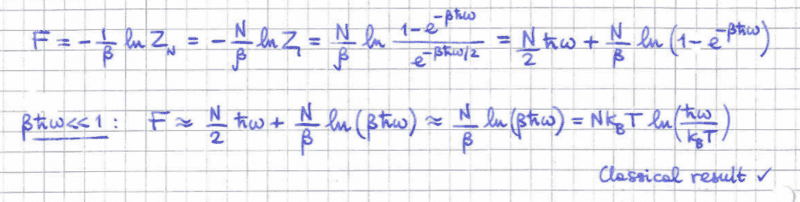
I am looking at the second line limit ##\beta (h/2\pi) \omega << 1 ##
2. Homework Equations
above
3. The Attempt at a Solution
Q1)In general in an expansion we neglect terms when we expand about some the variable taking small values of the function because the other terms are so small and so we get a good approximation from e.g first order terms. so in this case i see in the exponential expansion we have gone up to ##O(x=\beta (h/2\pi) \omega )## and the '1s' have cancelled. However, to me this makes sense if we were looking at ##\exp^{x}## but instead we are looking at ##e^{-x}## and when we raise to a negative exponent between ##0 < x <1 ## this is large, so why do we expand out?
for e.g i the log term in the 2nd term must be tending ##\to -\infty ## and I thought this is the reason we don't expand it out? or why do we not expand it out, I know in general you can't expand out ## \log (0) ## and it seems like we have a limiting case of this, but..thanks
Question attached.
I am looking at the second line limit ##\beta (h/2\pi) \omega << 1 ##
2. Homework Equations
above
3. The Attempt at a Solution
Q1)In general in an expansion we neglect terms when we expand about some the variable taking small values of the function because the other terms are so small and so we get a good approximation from e.g first order terms. so in this case i see in the exponential expansion we have gone up to ##O(x=\beta (h/2\pi) \omega )## and the '1s' have cancelled. However, to me this makes sense if we were looking at ##\exp^{x}## but instead we are looking at ##e^{-x}## and when we raise to a negative exponent between ##0 < x <1 ## this is large, so why do we expand out?
for e.g i the log term in the 2nd term must be tending ##\to -\infty ## and I thought this is the reason we don't expand it out? or why do we not expand it out, I know in general you can't expand out ## \log (0) ## and it seems like we have a limiting case of this, but..thanks