alan
- 4
- 0
I have known the interaction parameter of a certain liquid mixture
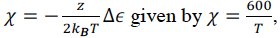
which has the phase behaviour can be described by the lattice model.
, is it possible for us to know the temperature at the critical point?
Besides, if we know the temperature at the critical point, can the volume fraction of the coexisting composition and that on the spinodal line at 273K be found?
Should it look like as follow?
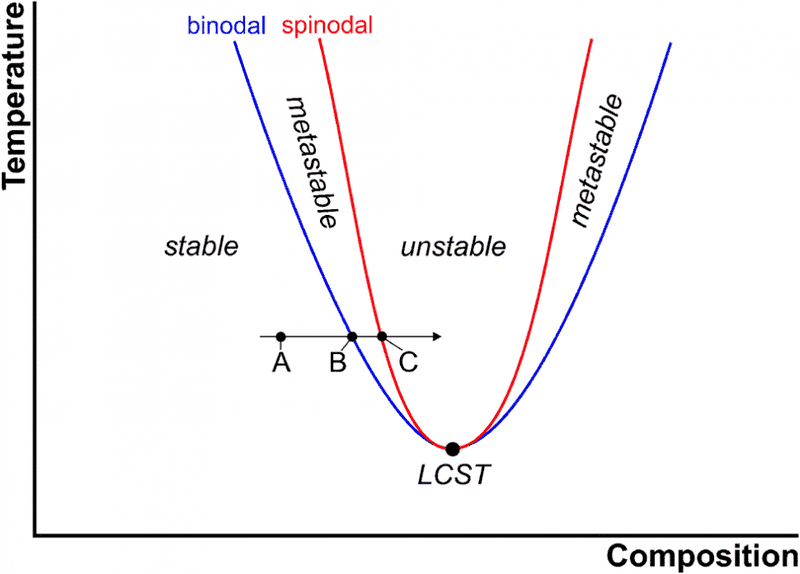
I don't know should the spinodal is drawn like this ?
I have found some links on the question mentioned, it is related to the field of statistical mechanics, thermodynamics, soft matter.
https://en.wikipedia.org/wiki/Critical_point_(thermodynamics
https://en.wikipedia.org/wiki/Spinodal
I put it here for your reference and I later review more.
which has the phase behaviour can be described by the lattice model.
, is it possible for us to know the temperature at the critical point?
Besides, if we know the temperature at the critical point, can the volume fraction of the coexisting composition and that on the spinodal line at 273K be found?
Should it look like as follow?
I don't know should the spinodal is drawn like this ?
I have found some links on the question mentioned, it is related to the field of statistical mechanics, thermodynamics, soft matter.
https://en.wikipedia.org/wiki/Critical_point_(thermodynamics
https://en.wikipedia.org/wiki/Spinodal
I put it here for your reference and I later review more.
Attachments
Last edited by a moderator: