seehuendchen
- 3
- 0
Homework Statement
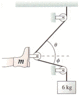
An accident victim with a broken leg is being placed in traction. The patient wears a special boot with a pulley attached to the sole. The foot and boot together have a mass of m = 3.4 kg, and the doctor has decided to hang a 6.0 kg mass from the rope. The boot is held suspended by the ropes and does not touch the bed. ϕ = 10°.
(a) Determine the amount of tension in the rope by using Newton's laws to analyze the hanging mass.
(b) The net traction force needs to pull straight out on the leg. What is the proper angle θ for the upper rope?
(c) What is the net traction force pulling on the leg? (Hint: If the pulleys are frictionless, which we will assume, the tension in the rope is constant from one end to the other.)
Homework Equations
F=ma
W=mg
The Attempt at a Solution
I was easily able to use W=mg to find the tension in the rope to be 58.8N.
After that, I am lost.
I know the Fnet(y) should be zero since the boot is pulling straight out, but I can't get any further than that...
I also imagine somehow that i will find acceleration along the x-axis, then because the system is in equilibrium (the leg will not move), I will use acceleration and the mass of the boot to find the net traction force.
I really need some help finding the angle theta. Thanks!