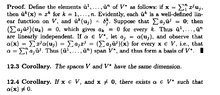The Dual Space and Covectors .... Browdwer, Theorem 12.2 and Corollaries ....

[Math Amateur]

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 12: Multilinear Algebra and am specifically focused on Section 12.1: Vectors and Tensors ...

I need help in fully understanding Corollary 12.4 to Theorem 12.2 ... ...

Theorem 12.2 and its corollaries read as follows:
View attachment 8795
View attachment 8796In the above text from Browder, we read the following:

" ... ... 12.4 Corollary. If $$x \in V$$, and $$x \neq 0$$, there exists $$\alpha \in V^*$$ such that $$\alpha (x) \neq 0$$ ... ... "
Can someone please demonstrate a formal and rigorous proof for Corollary 12.4 ...?
Help will be appreciated ... ...

Peter

 

[Euge]

Hi Peter,

Given a nonzero element $\bf{x}$ of $V$, the set $\{\bf{x}\}$ is linearly independent; this set thus extends to a basis of $V$. By the theorem, the basis has a dual basis in $V^*$ in which one element, call it $\alpha$, satisfies $\alpha(\mathbf{x}) = 1$. In particular, $\alpha(\mathbf{x}) \neq 0$.

 

[steenis]

Or put it otherwise, let
$$x=\sum_{j=1}^{n} \xi^j u_j \in V$$
in terms of the basis $\{u_1, \cdots, u_n \} $ of $V$, such that $\alpha(x)=0$ for all $\alpha \in V^*$

Then for each member $\bar{u}^i$ of the basis $\{ \bar{u}^1, \cdots, \bar{u}^n\}$ of $V^*$ we have
$$ \bar{u}^i(x)=\xi^i=0$$

Therefore $x=0$

Edit: I changed the positions of some indices.